
【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2﹣12n+36+|n﹣2m|=0.

(1)求A、B两点的坐标;
(2)若点D为AB中点,延长DE交x轴于点F,在ED的延长线上取点G,使DG=DF,连接BG.
①BG与y轴的位置关系怎样?说明理由; ②求OF的长;
(3)如图2,若点F的坐标为(10,10),E是y轴的正半轴上一动点,P是直线AB上一点,且P的横坐标为6,是否存在点E使△EFP为等腰直角三角形?若存在,求出点E的坐标;若不存在,说明理由.
【答案】(1)A(3,0),B(0,6);(2)①BG与y轴垂直,理由见解析,②OF=1.5(3)存在点E(0,4),使△EFP为等腰直角三角形
【解析】
(1)先求出m,n的值,即可得出结论;
(2)①先判断出△BDG≌△ADF,得出BG=AF,∠G=∠DFA,最后根据平行线的性质得出∠DFA=45°,∠G=45°,即可得出结论;
②利用等腰三角形的性质,建立方程即可得出结论;
(3)先求出点P坐标,进而得出Rt△FME≌Rt△ENP,进而得出求出OE,即可得出结论.
(1)由n2-12n+36+|n-2m|=0.得:(n-6)2+|n-2m|=0,
∴n=6,m=3,
∴A(3,0),B(0,6).
(2)①BG⊥y轴.
在△BDG与△ADF中,
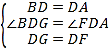
∴△BDG≌△ADF
∴BG=AF,∠G=∠DFA
∵OC平分∠ABC,
∴∠COA=45°,
∵DE∥OC,
∴∠DFA=45°,∠G=45°.
∵∠FOE=90°,
∴∠FEO═45°
∵∠BEG=45°,
∴∠EBG=90°,
即BG与y轴垂直.
②从①可知,BG=FA,△BDE为等腰直角三角形.
∴BG=BE.
设OF=x,则有OE=x,3+x=6-x,解得x=1.5,
即:OF=1.5.
(3)∵A(3,0),B(0,6).
∵直线AB的解析式为:y=-2x+6,
∵P点的横坐标为6,
故P(6,-6)
要使△EFP为等腰直角三角形,必有EF=EP,且∠FEP═90°,
如图2,过F、P分别向y轴作垂线垂足分别为M、N.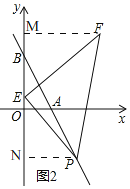
∵∠FEP═90°
∴∠FEM+∠PEN=90°,又∠FEM+∠MFE=90°
∴∠PEN=∠MFE
∴Rt△FME≌Rt△ENP
∴ME=NP=6,
∴OE=10-6=4.
即存在点E(0,4),使△EFP为等腰直角三角形


科目:初中数学 来源: 题型:
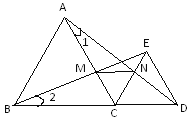
【题目】如图,点C为线段BD上的点,分别以BC,CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于点M,连接AD交CE于点N,连接MN.试说明:(1)![]() ;(2)
;(2)![]() 为等边三角形.
为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C>∠B,AD,AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数;
(2)∠DAE与∠C-∠B有何关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线.
(1)求证:CE=CB;
(2)连接AF,BF,求∠ABF的正弦值;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,∠MAN=45°,连接BD与AM,AN分别交于E,F点,则下列结论正确的有_____.
①MN=BM+DN
②△CMN的周长等于正方形ABCD的边长的两倍;
③EF2=BE2+DF2;
④点A到MN的距离等于正方形的边长
⑤△AEN、△AFM都为等腰直角三角形.
⑥S△AMN=2S△AEF
⑦S正方形ABCD:S△AMN=2AB:MN
⑧设AB=a,MN=b,则![]() ≥2
≥2![]() ﹣2.
﹣2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,关于点![]() 的图象变化有以下说法:
的图象变化有以下说法:
①点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的坐标为
的坐标为![]()
②点![]() 与点
与点![]() 关于原点对称
关于原点对称
③把点![]() 先向右平移
先向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度得到点
个单位长度得到点![]()
④把点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() ,得到点
,得到点![]()
其中,正确的说法是( )
A. ①③④ B. ①②③④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我省在修建泛亚铁路时遇到一座山,要从![]() 地向
地向![]() 地修一条隧道(
地修一条隧道(![]() ,
,![]() 在同一水平面上),为了测量
在同一水平面上),为了测量![]() ,
,![]() 两地之间的距离,某工程师乘坐热气球从
两地之间的距离,某工程师乘坐热气球从![]() 地出发垂直上升
地出发垂直上升![]() 米到达
米到达![]() 处,在
处,在![]() 处观察
处观察![]() 地的俯角为
地的俯角为![]() ,然后保持同一高度向前平移
,然后保持同一高度向前平移![]() 米到达
米到达![]() 处,在
处,在![]() 处观察
处观察![]() 地的俯角为
地的俯角为![]() ,则
,则![]() 、
、![]() 两地之间的距离为多少米?(参考数据:
两地之间的距离为多少米?(参考数据:![]() ;结果保留整数)
;结果保留整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com