
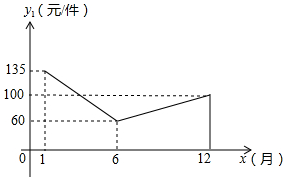
 某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.
某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.分析 (1)根据待定系数法,可得函数解析式;
(2)根据销售额减去销售成本,可得销售利润,根据函数的性质,可得最大利润.
解答 解:(1)设销售价格y1(元/件)与销售月份x(月)之间的函数关系式为y1=kx+b (6≤x≤12),
函数图象过(6,60)、(12,100),则
$\left\{\begin{array}{l}{6k+b=60}\\{12k+b=100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{20}{3}}\\{b=20}\end{array}\right.$,
故销售价格y1(元/件)与销售月份x(月)之间的函数关系式y1=$\frac{20}{3}$x+20 (6≤x≤12且x为整数);
(2)由题意得w=y1•y3-y2•y3即
w=($\frac{20}{3}$x+20)•(10x+20)-$\frac{14}{3}$x•(10x+20)
化简,得
w=20x2+240x+400,
∵a=20,x=-$\frac{b}{2a}$=-$\frac{240}{2×20}$=-6是对称轴,
当x>-6时,w随x的增大而增大,
∴当x=12时,销售量最大,W最大=20×122+240×12+400=6160,
答:12月份利润最大,最大利润是6160元.
点评 本题考查了二次函数的应用,利用了待定系数法求解析式,解题的关键是搞清楚利润,销售量,每件的利润之间的关系,学会利用函数的性质的最确定最值问题,所以中考常考题型.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:解答题
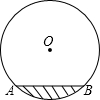 如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,
如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.6m,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
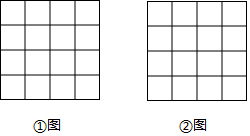 如图,正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,以格点为顶点分别按下列要求画图.
如图,正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,以格点为顶点分别按下列要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
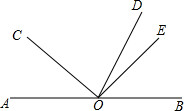 如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 线段有两个端点 | B. | 两点之间,直线最短 | ||
| C. | 两点之间,线段最短 | D. | 线段可以比较大小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com