
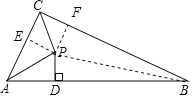
【题目】如图,在△ABC中,∠ACB=90°,∠ACB与∠CAB的平分线交于点P,PD⊥AB于点D,若△APC与△APD的周长差为![]() ,四边形BCPD的周长为12+
,四边形BCPD的周长为12+![]() ,则BC等于______.
,则BC等于______.

【答案】6
【解析】
过P作PE⊥AC于E,PF⊥BC于F,连接PB,根据已知条件得到PB平分∠ABC,推出矩形CEPF是正方形,设CE=x,得到CF=PE=x,PC![]() x,根据角平分线的性质得到PE=PD,根据全等三角形的性质得到AD=AE,同理BD=BF,根据已知条件即可得到结论.
x,根据角平分线的性质得到PE=PD,根据全等三角形的性质得到AD=AE,同理BD=BF,根据已知条件即可得到结论.
过P作PE⊥AC于E,PF⊥BC于F,连接PB.
∵∠ACB与∠CAB的平分线交于点P,∴PB平分∠ABC.
∵∠ACB=90°,∴四边形CEPF是矩形.
∵CP是∠ACB的角平分线,∴PF=PE,∴矩形CEPF是正方形,∴设CE=x,∴CF=PE=x,PC![]() x.
x.
∵AP是∠CAB的角平分线,∴PE=PD.
∵AP=AP,∴Rt△PAE≌Rt△PAD(HL),∴AD=AE,同理BD=BF.
∵△APC与△APD的周长差为![]() ,∴PC
,∴PC![]() ,∴CE=CF=PD=1.
,∴CE=CF=PD=1.
∵四边形BCPD的周长为12![]() ,∴2BF+PC+PD+CF=12
,∴2BF+PC+PD+CF=12![]() ,∴BF
,∴BF![]() 5,∴BC=6.
5,∴BC=6.
故答案为:6.


科目:初中数学 来源: 题型:
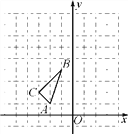
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;
(2)若点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车在行驶的过程中速度往往是变化的,如图表示一辆汽车的速度随时间变化而变化的情况.
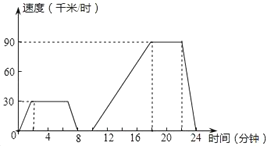
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车出发8min到10min之间可能发生了什么情况?
(4)求汽车从出发后第18分钟到第22分钟行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下面的说理过程和理由补充完整.
已知:如图,AB∥CD,∠B=∠D,说明:BF∥DE.

解:AB∥CD.(已知)
∴∠A=∠C.( ____①___)
在△ABF和△CDE中
∵∠B=∠D=90°,(已知)
∴∠A+∠AFB=90°
∠C+___②___=90°.(直角三角形的两个锐角互余)
又∵∠A=∠C,(已证).
∴∠AFB=____③_____.(_____④_____)
∴BF∥DE.( ___⑤_____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D,E在AC的同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
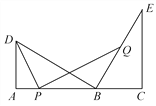
(1)求证:AC=AD+CE;
(2)若AD=3,AB=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q,当点P与A,B两点不重合时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,准备用1200元钱(全部用完)购买A,B两种笔记本作为奖品,已知A,B两种每本分别为12元和20元,设购入A种x本,B种y本.
(1)求y关于x的函数表达式.
(2)若购进A种的数量不少于B种的数量.
①求至少购进A种多少本?
②根据①的购买,发现B种太多,在费用不变的情况下把一部分B种调换成另一种C,调换后C种的数量多于B种的数量,已知C种每本8元,则调换后C种至少有______本(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
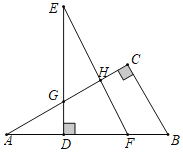
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边上一点,DE⊥AB,且DE=AC,DE与AC交于点G,过点E作FE∥BC交AB于点F,交AC于点H.
(1)求证:△ABC≌△EFD;
(2)若∠EFD=55°,求∠DGH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 分别为两条平行线
分别为两条平行线![]() 上的一点,
上的一点,![]() 于
于![]() .
.
(1)如图1,直接写出![]() 和
和![]() 之间的数量关系;
之间的数量关系;
(2)如图2,连接![]() ,过点
,过点![]() 分别作
分别作![]() 和
和![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②探究![]() 和
和![]() 的数量关系并加以证明.
的数量关系并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com