
��ͼ�������߹�x��������A(9,0),C(-3,0),����y�ύ�ڵ�B(0,-12).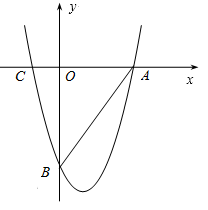
��1���������ߵĽ���ʽ��
��2��������P�ӵ�A��������ÿ��2����λ������AC�����˶���ͬʱ����Q�ӵ�B��������ÿ��1����λ������BA�����˶�������P�����C��ʱ������ͬʱֹͣ�˶�.�ʵ�tΪ��ֵʱ����APQ�ס�AOB��
��3����MΪ�߶�AB��һ�����㣬����M��MNƽ����y�ύ�������ڵ�N��
���Ƿ���������ĵ�M��ʹ���ı���OMNBǡΪƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�ڵ���M�˶����δ�ʱ���ı���CBNA�������������ʱ��M�����꼰�ı���CBNA��������ֵ��
��1��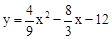 ����2��
����2�� ����3���ٲ����ڣ��ڵ���M�˶�����
����3���ٲ����ڣ��ڵ���M�˶�����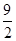 ����6��ʱ���ı���CBNA���������ı���CBNA��������ֵΪ
����6��ʱ���ı���CBNA���������ı���CBNA��������ֵΪ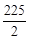 ��
��
���������������1��Ӧ�ô���ϵ�������轻��ʽ��⣻
��2���������������ε�������⼴�ɣ�
��3������MN��OB��12��ʽ������һԪ���η��̸����б�ʽС��0�ó������������ĵ�M��ʹ���ı���OMNBǡΪƽ���ı��ν��ۣ�������������x�Ķ��κ�����ϵʽ��Ӧ�ö��κ�����ֵԭ����⼴��.
�����������1���������߹�x��������A(9,0),C(-3,0)�����������߽���ʽΪ��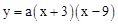 .
.
�֡�B(0,-12) ��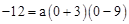 �����a=
�����a= ��
��
�������ߵĽ���ʽΪ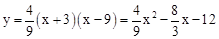 .
.
��2����OA=9��OB=12����AB=15.
�ߵ�P���ٶ���ÿ��2����λ����Q���ٶ���ÿ��1����λ����AP��2t��AQ��15��t.
�֡�AC=12����0��t��6.
�ߡ�APQ�ס�AOB����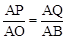 ����
���� �����
�����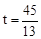 .
.
�൱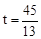 ʱ����APQ�ס�AOB.
ʱ����APQ�ס�AOB.
��3������ֱ��AB�ĺ�����ϵʽΪ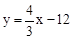 ��
��
���M�ĺ�����Ϊx����M��x��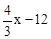 ����N��x��
����N��x�� ����
����
�����ı���OMNBΪƽ���ı��Σ���MN��OB��12
��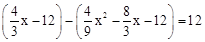 ����x2��9x��27��0.
����x2��9x��27��0.
�ߡ���0����˷�����ʵ����.
����������ĵ�M��ʹ���ı���OMNBǡΪƽ���ı��Σ�
�ڡ�S�ı���CBNA=S��ACB+S��ABN="72+" S��ABN
��S��AOB��54��S��OBN��6x��S��OAN��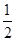 ��9��
��9�� ����2x2��12x��54
����2x2��12x��54
��S��ABN��S��OBN��S��OAN��S��AOB��6x��(��2x2��12x��54)��54����2x2��18x��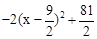 .
.
�൱x�� ʱ��S��ABN���ֵ��
ʱ��S��ABN���ֵ�� ����ʱM��
����ʱM��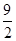 ����6��
����6��
S�ı���CBNA���=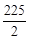 ��
��
���㣺1.˫�������⣻2.����ϵ������Ӧ�ã�3.�����ϵ�������뷽�̵Ĺ�ϵ��4. ���������ε����ʣ�5. ƽ���ı��ε��ж���6. һԪ���η��̸����б�ʽ��7.���κ�����ֵ.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪��ƽ��ֱ������ϵ�У��ı���ABCO�����Σ���BC��AO������A��6��0����B��3�� ������AOC=60�㣬����P�ӵ�O��ÿ��2����λ���ٶ����A�˶�������QҲͬʱ�ӵ�B��B��C��O����·��ÿ��1����λ���ٶ����O�˶�������P����A��ʱ����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ��Ϊt���룩��
������AOC=60�㣬����P�ӵ�O��ÿ��2����λ���ٶ����A�˶�������QҲͬʱ�ӵ�B��B��C��O����·��ÿ��1����λ���ٶ����O�˶�������P����A��ʱ����QҲ��ֹ֮ͣ�����P��Q�˶���ʱ��Ϊt���룩��

��1�����C�����꼰����ABCO�������
��2������Q��CO�����˶�ʱ�����OPQ�����S���˶�ʱ��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3����O��P��QΪ������������ܹ���ֱ�������������ܣ������t��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������y= x2+mx+n��x����A��B���㣬��y���ڵ�C����P�����Ķ��㣬��A�������ǣ�1��0������B�������ǣ���3��0����
x2+mx+n��x����A��B���㣬��y���ڵ�C����P�����Ķ��㣬��A�������ǣ�1��0������B�������ǣ���3��0����
��1����m��n��ֵ��
��2����ֱ��PC�Ľ���ʽ��
[��ܰ��ʾ��������y=ax2+bx+c��a��0���Ķ�������Ϊ���� ��
�� ��]��
��]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�̵꽫����Ϊÿ��80Ԫ��ij����Ʒ��ÿ��100Ԫ���ۣ�ÿ����۳�100���������г����飬����������Ʒÿ��ÿ����1Ԫ�����������Ϳ�����10��.
��1����ÿ����Ʒ�����ۼ� Ԫ���ۺ�ÿ������ Ԫ��ÿ����۳� �����ú�
Ԫ���ۺ�ÿ������ Ԫ��ÿ����۳� �����ú� �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2������̵�Ϊ��ÿ��������2160Ԫ����ôÿ����ƷӦ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ��� ��ͼ����A��2����3����B����1��0����
��ͼ����A��2����3����B����1��0����
��1������κ����Ľ���ʽ��
��2���۲캯��ͼ��Ҫʹ�ö��κ�����ͼ���� ��ֻ��һ�����㣬Ӧ��ͼ����
��ֻ��һ�����㣬Ӧ��ͼ���� ������ƽ�Ƽ�����λ��
������ƽ�Ƽ�����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
������ ������A(4,0),B(2,2),����OB,AB��
������A(4,0),B(2,2),����OB,AB��
(1)��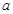 ��
�� ��ֵ��
��ֵ��
(2)��֤����OAB�ǵ���ֱ�������Σ�
(3)����OAB�Ƶ�O��˳ʱ�뷽����תl35��õ���OA��B��,д��A��B����е�P�ij��꣮���жϵ�P�Ƿ��ڴ���������,��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���֪������ ��
�� ����A��2��0����B��6��0�����㣬��
����A��2��0����B��6��0�����㣬�� ���ڵ�C��0��
���ڵ�C��0��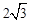 ��.
��.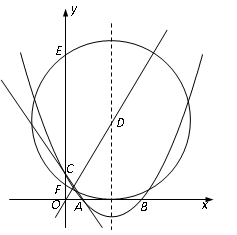
��1����������ߵĽ���ʽ��
��2�����������ߵĶԳ�����ֱ��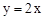 ���ڵ�D������D��x�����У���D��
���ڵ�D������D��x�����У���D�� ���ڵ�E��F���㣬���ӻ�EF����Բ�ĽǵĶ�����
���ڵ�E��F���㣬���ӻ�EF����Բ�ĽǵĶ�����
��3��PΪ���������ڵڶ�����ͼ���ϵ�һ�㣬PG��ֱ�� �ᣬ����Ϊ��G����ȷ��P���λ�ã�ʹ�á�PGA�������ֱ��AC��Ϊ1�U2������.
�ᣬ����Ϊ��G����ȷ��P���λ�ã�ʹ�á�PGA�������ֱ��AC��Ϊ1�U2������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
������ ���㣨2��-2���ͣ�-1��10������x�ύ��A��B���㣬��y�ύ��C�㣮
���㣨2��-2���ͣ�-1��10������x�ύ��A��B���㣬��y�ύ��C�㣮
��1���������ߵĽ���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����ͼ,ֱ��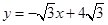 ��x���ཻ�ڵ�A,��ֱ��
��x���ཻ�ڵ�A,��ֱ�� �ཻ�ڵ�P.����E��ԭ��O����,��ÿ��1����λ���ȵ��ٶ�����OPA��·�����A�����˶���E�����O,A�غϣ�,����E�ֱ���EF��x����F,EB��y����B.���˶�t��ʱ,����EBOF���OPA�ص��������ΪS.
�ཻ�ڵ�P.����E��ԭ��O����,��ÿ��1����λ���ȵ��ٶ�����OPA��·�����A�����˶���E�����O,A�غϣ�,����E�ֱ���EF��x����F,EB��y����B.���˶�t��ʱ,����EBOF���OPA�ص��������ΪS.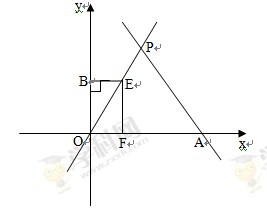
��1�����P������;
��2�����жϡ�OPA����״��˵������;
��3����̽��S��t֮��ĺ�����ϵʽ,��ָ��t��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com