
����Ŀ����ͼ�����ھ���ABCD�У�AB��![]() ��BC��3����BC����ȡ����E��F����E�ڵ�F����ߣ�����EFΪ�������ȱߡ�PEF������Pǡ����AD�ϣ�ֱ��PE��PF�ֱ�ֱ��AC�ڵ�G��H��
��BC��3����BC����ȡ����E��F����E�ڵ�F����ߣ�����EFΪ�������ȱߡ�PEF������Pǡ����AD�ϣ�ֱ��PE��PF�ֱ�ֱ��AC�ڵ�G��H��
��1�����PEF�ı߳���
��2������PEF�ı�EF���߶�CB���ƶ����Բ��룺PH��BE�к�������ϵ����֤�������Ľ��ۣ�
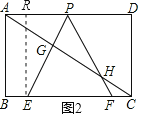
��3������PEF�ı�EF������CB���ƶ����ֱ���ͼ����ͼ����ʾ��CF��1��P����A�غϣ�����2���еĽ��ۻ�����������������ֱ��д���㷢�ֵ��½��ۣ�
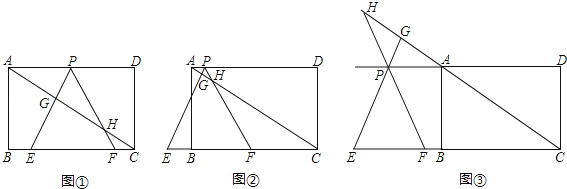
���𰸡���1����PEF�ı߳�Ϊ2����2��PH��BE=1��֤�����̼���������3�����۲���������1��CF��2ʱ��PH=1��BE����2��CF��3ʱ��PH=BE��1��
��������
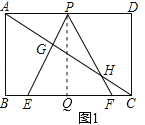
�����P��PQ��BC������ΪQ�����ı���ABCDΪ���Σ��õ���BΪֱ�ǣ���AD��BC���õ�PQ=AB������PEFΪ�ȱ������Σ����������ߺ�һ���õ���FPQΪ30������Rt��PQF�У����QFΪx����PF=2x����PQ�ij������ݹ��ɶ����г�����x�ķ��̣����x��ֵ�����ɵõ�PF�ij�����Ϊ�ȱ������εı߳���
PH��BE=1����E��ER��ֱ��AD����ͼ��ʾ������֤����APHΪ���������Σ��ڸ��ݾ��εĶԱ�ƽ�еõ�һ���ڴ�����ȣ��ɵ���APE=60������Rt��PER�У���REP=30��������ֱ���������У�30�������Ե�ֱ�DZߵ���б�ߵ�һ�룬��PE���PR����PA=PH����PH��BE=PA��BE=PA��AR=PR�����ɵõ����߶εĹ�ϵ��
������PEF�ı�EF������CB���ƶ�ʱ��2���еĽ��۲��������ɣ�2���Ľ���˼·��֪��1��CF��2ʱ��PH=1��BE����2��CF��3ʱ��PH=BE��1��
�����������1����P��PQ��BC��Q����ͼ1���� ���ı���ABCD�Ǿ��Σ� ���B=90������AB��BC��
����AD��BC�� ��PQ=AB=![]() �� �ߡ�PEF�ǵȱ������Σ� ���PFQ=60����
�� �ߡ�PEF�ǵȱ������Σ� ���PFQ=60����
��Rt��PQF�У���FPQ=30���� ��PF=2x��QF=x��PQ=![]() �����ݹ��ɶ����ã�
�����ݹ��ɶ����ã�![]() ��
��
��ã�x=1����PF=2�� ���PEF�ı߳�Ϊ2��
��2��PH��BE=1���������£� ����Rt��ABC�У�AB=![]() ��BC=3�� ���ɹ��ɶ�����AC=2
��BC=3�� ���ɹ��ɶ�����AC=2![]() ��
��
��CD=![]() AC�� ���CAD=30�� ��AD��BC����PFE=60���� ���FPD=60���� ���PHA=30��=��CAD��
AC�� ���CAD=30�� ��AD��BC����PFE=60���� ���FPD=60���� ���PHA=30��=��CAD��
��PA=PH�� ���APH�ǵ��������Σ� ��ER��AD��R����ͼ2�� Rt��PER�У���RPE=60���� ��PR=![]() PE=1��
PE=1��
��PH��BE=PA��BE=PR=1��
��3�����۲�������
��1��CF��2ʱ��PH=1��BE�� ��2��CF��3ʱ��PH=BE��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ�
��b��0����4a+2b+c��0����a��b+c��0������a+c��2��b2��������ȷ�Ľ�����
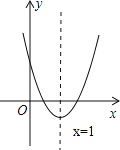
A���٢� B���٢� C���٢ۢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
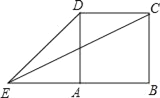
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1���ӳ�BA��E��ʹAE��1������EC��ED����sin��CED����������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��y1=-![]() x+m��y�ύ�ڵ�A(0��6)��ֱ��l2��y2=kx+1�ֱ���x�ύ�ڵ�B(-2��0)����y�ύ�ڵ�C������ֱ��l1��l2�ཻ�ڵ�D������AB��
x+m��y�ύ�ڵ�A(0��6)��ֱ��l2��y2=kx+1�ֱ���x�ύ�ڵ�B(-2��0)����y�ύ�ڵ�C������ֱ��l1��l2�ཻ�ڵ�D������AB��
(1)����ֱ��l1��l2����D�����ꣻ
(2)���ABD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���OBC�Ķ���ֱ�ΪO��0��0����B��3����1����C��2��1����
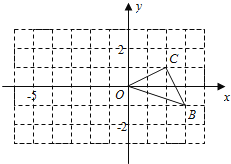
��1���Ե�O��0��0��Ϊλ�����ģ���������2��1��λ�����ĵ���ཫ��OBC�Ŵ�Ϊ��OB��C�����Ŵ���B��C����Ķ�Ӧ��ֱ�ΪB����C����������OB��C������д����B����C�������꣺B���� �� ����C���� �� ����
��2������1���У�����M��x��y��Ϊ�߶�BC����һ�㣬д���仯���M�Ķ�Ӧ��M���������� �� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��RtABC�У���C=90�㣬��A=30������ֱ��AC���ҵ�P��ʹ��ABP�ǵ��������Σ����APB�Ķ���Ϊ_______________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽס��ҡ�������4��ͬѧ�������ȡͬѧ�μ�ѧУ����̸��
(1)��ȡһ��ͬѧ�� ǡ���Ǽĸ���Ϊ
(2) ��ȡ����ͬѧ����������еĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
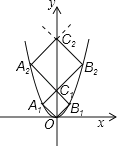
����Ŀ����ͼ����֪��A1��A2������A2011�ں���y=x2λ�ڵڶ�����ͼ���ϣ���B1��B2������B2011�ں���y=x2λ�ڵ�һ����ͼ���ϣ���C1��C2������C2011��y����������ϣ����ı���OA1C1B1��C1A2C2B2������C2010A2011C2011B2011���������Σ���������C2010A2011C2011B2011�ı߳�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У�AB=AC����DΪBC�е㣮��MDN=900����MDN�Ƶ�D��ת��DM��DN�ֱ����AB��AC����E��F���㣮���н���
��(BE+CF)=![]() BC����
BC����![]() ����
����![]() AD��EF����AD��EF����AD��EF���ܻ���ƽ�֣�
AD��EF����AD��EF����AD��EF���ܻ���ƽ�֣�
������ȷ���۵ĸ����ǣ� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com