
 如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连结DE,BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2$\sqrt{3}$,BC=2$\sqrt{5}$,则图中阴影部分图形的面积和为2$\sqrt{15}$.
如图,在矩形ABCD中,点E,F分别是AB,CD的中点,连结DE,BF,分别取DE,BF的中点M,N,连结AM,CN,MN,若AB=2$\sqrt{3}$,BC=2$\sqrt{5}$,则图中阴影部分图形的面积和为2$\sqrt{15}$. 分析 利用三角形中线的性质以及平行线的性质得出S△AEM=S△AMD,S△BNC=S△FNC,S四边形EBNM=S四边形DMNF,即可得出答案.
解答 解:∵点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,
∴S△AEM=S△AMD,S△BNC=S△FNC,S四边形EBNM=S四边形DMNF,
∴图中阴影部分的面积=$\frac{1}{2}$×AB×BC=$\frac{1}{2}$×2$\sqrt{3}$×2$\sqrt{5}$=2$\sqrt{15}$.
故答案为:2$\sqrt{15}$.
点评 此题主要考查了矩形的性质以及三角形中线的性质,得出图中阴影部分的面积=$\frac{1}{2}$矩形ABCD是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
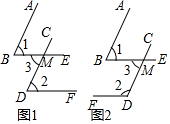 在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结论图形完成以下探究过程:
在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结论图形完成以下探究过程:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1<mx-n的解集为( )
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1<mx-n的解集为( )| A. | x<m | B. | x<2 | C. | x<1 | D. | x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com