解:(1)不变,因为四边形AEDF为平行四边形,平行四边形的对角相等;
(2)在?AEDF中,DF=AE,AF=DE,ED∥AC
∴∠EDB=∠C,
∵在△ABC中,AB=AC,
∴∠B=∠C,
∴∠B=∠EDB,
∴BE=ED=AF,
∴C?AEDF=2(AE+DE)=2(AE+BE)=2AB=20,
即?AEDF的周长等于等腰三角形的两腰之和,周长为20cm;
(3)?AEDF的周长保持不变,周长等于常数20cm.
分析:(1)由题可知,四边形AEDF为平行四边形,∠EDF=∠A,所以在D点运动过程中,只要∠A度数不发生变化,它的度数就不变;
(2)平行四边形AEDF中,FD=AE,AF=ED,因为ED和AC平行,所以∠EDB和∠C相等,又在等腰三角形ABC中,∠B=∠C,所以BE=DE,同理,AF=BE,即平行四边形AEDF周长等于AB的2倍20;
(3)在D点运动过程中,虽然平行四边形AEDF形状会发生变化,但是线段之间的和差关系不变,即平行四边形AEDF周长永远等于三角形ABC腰长的2倍.
点评:本题主要考查了平行四边形中对边相等的性质及应用,以及等腰三角形的等角对等边的性质,难易程度适中.

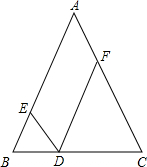 四边形.
四边形.

 24、如图,AB=AC=AD.
24、如图,AB=AC=AD.