
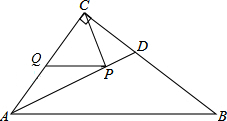
 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4. 分析 作辅助线,构建PC+PQ的最小值,即CM的值,根据面积法求出CM的长,即PC+PQ的最小值.
解答  解:如图,过C作CM⊥AB,交AD于P,交AB于M,过P作PQ⊥AC于Q,
解:如图,过C作CM⊥AB,交AD于P,交AB于M,过P作PQ⊥AC于Q,
∵AD是∠BAC的平分线,
∴PQ=PM,
这时PC+PQ有最小值,即CM的长度,
∵∠ACB=90°,∠B=30°,BC=8,
tan30°=$\frac{AC}{BC}$,cos30°=$\frac{BC}{AB}$,
∴AC=8×$\frac{\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$,AB=$\frac{8}{\frac{\sqrt{3}}{2}}$=$\frac{16\sqrt{3}}{3}$,
∴S△ACB=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM,
∴$\frac{8\sqrt{3}}{3}$×8=$\frac{16\sqrt{3}}{3}$•CM,
∴CM=4,
∴PC+PQ的最小值为4,
故答案为:4.
点评 本题考查了最短路径问题和含30°角的直角三角形的性质,在直角三角形,30°角所对的直角边是斜边的一半,也可以利用30°角的三角函数列式求边长;凡是涉及最短距离的问题,一方面考虑垂线段最短,如本题,另一方面利用所学轴对称变换来解决,作点关于某直线的对称点.


科目:初中数学 来源: 题型:选择题
| A. | 2 011 | B. | 2 015 | C. | 2 014 | D. | 2 016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
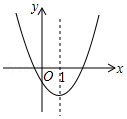 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
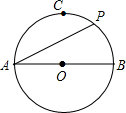 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$的中点,则∠PAB的度数( )| A. | 30° | B. | 25° | C. | 22.5° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$a元 | B. | $\frac{100}{81}$a元 | C. | a(1-10%)2元 | D. | a(1-10)元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com