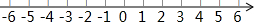练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．在数轴上表示下列各数，并按从大到小的顺序排列，用“＞”连接起来：
    |+3|，4$\frac{1}{2}$，-|-2|，0，-5．

    分析 根据数轴是表示数的一条直线，可把数在数轴上表示出来，根据数轴上的点表示的数右边的总比左边的大，可得答案．

    解答 解：如图，
    数轴上的点表示的数右边的总比左边的大，得
    4$\frac{1}{2}$＞|+3|＞0＞-|-2|＞-5．

    点评 本题考查了有理数大小比较，利用数轴上的点表示的数右边的总比左边的大是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．正方形ABCD的边长为a，以相邻的两边为直径分别画两个半圆，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

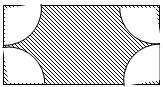    18．如图是某居民小区的一块长为b米，宽为2a米的长方形空地，为了美化环境，准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台，然后在花台内种花，其余种草．如果建造花台及种花费用每平方米需要资金100元，种草每平方米需要资金50元，那么美化这块空地共需资金多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算题：
    （1）（-3a3）2a4                         
    （2）（-x）11÷（-x）9
    （3）7a（2ab-3b2）               
    （4）（x-3y）（x+3y）
    （5）（x2）3-x4•x2
    （6）（2x+1）（x-3）-（x-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．定义：将分母中的根号化去的过程叫做分母的过程叫做分母有理化．
    如：将$\frac{2}{{\sqrt{5}-\sqrt{3}}}$分母有理化．
    解：原式=$\frac{{2（{\sqrt{5}+\sqrt{3}}）}}{{（{\sqrt{5}-\sqrt{3}}）（{\sqrt{5}+\sqrt{3}}）}}$=（${\sqrt{5}$+$\sqrt{3}}$）．
    运用上面的方法解决问题：
    （1）将$\frac{2}{{\sqrt{3}+2}}$分母有理化．
    （2）化简：$\frac{1}{{1+\sqrt{2}}}$+$\frac{1}{{\sqrt{2}+\sqrt{3}}}$+$\frac{1}{{\sqrt{3}+\sqrt{4}}}$+…+$\frac{1}{{\sqrt{2015}+\sqrt{2016}}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

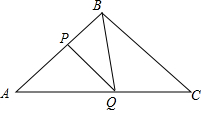    12．如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x秒．
    （1）当x为何值时，PQ∥BC；
    （2）当$\frac{{S}_{△BCQ}}{{S}_{△ABC}}$=$\frac{1}{3}$时，求$\frac{{S}_{△APQ}}{{S}_{△BPQ}}$的值；
    （3）△APQ能否与△CQB相似？若能，求出时间x的值；若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．一个n边形共有20条对角线，则n的值为（　　）
    A．5B．6C．8D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．计算：
    （1）$\sqrt{（-3）^{2}}$=3，
    （2）（$\sqrt{6}$）2=6，
    （3）$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$=$\sqrt{3}$，
    （4）$\sqrt{2}$（2$\sqrt{2}$-$\sqrt{5}$）=4-$\sqrt{10}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和．如23=3+5，33=7+9+11，43=13+15+17+19，…，若m3“分裂”后，其中有一个奇数是211，则m的值是15．

    查看答案和解析>>

    同步练习册答案