
 如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )
如图,在直角三角形ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,连结AD、AE,则下列结论中不成立的是( )| A. | AD∥BE,AD=BE | B. | ∠ABE=∠DEF | ||
| C. | ED⊥AC | D. | △ADE为等边三角形 |
分析 利用平移的性质可对A选项和B选项进行判断;先利用平移的性质得到AB∥DE,再利用AB⊥AC和平行线的性质可判断AC⊥DE,从而可对C选项进行判断;利用AB=DE,AD=BE,可对D选项进行判断.
解答 解:∵△ABC沿直线BC向右平移2.5个单位长度得到△DEF,
∴AD∥BE,AD=BE=2.5,A选项的结论正确;
∠ABC=∠DEF,B选项的结论正确;
∵△ABC沿直线BC向右平移2.5个单位长度得到△DEF,
∴AB∥DE,
而AB⊥AC,
∴DE⊥AC,C选项的结论正确;
∵AB=DE,AD=BE,
没有条件得出DE=AD,D选项的结论错误.
故选D.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 这500名考生是总体的一个样本 | B. | 每位考生是个体 | ||
| C. | 500名考生是总体 | D. | 这种调查是抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
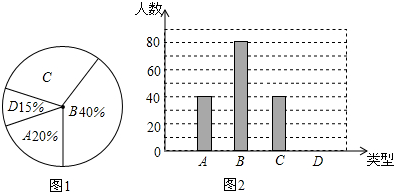
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com