
 如图,在平面直角坐标系xOy中,正方形ABCD的顶点A在直线l:y=2x上,AB⊥x轴,顶点B的坐标为(2,1).
如图,在平面直角坐标系xOy中,正方形ABCD的顶点A在直线l:y=2x上,AB⊥x轴,顶点B的坐标为(2,1).分析 (1)将x=2代入y=2x,可求得y=4,从而可求得AB=3,于是可求得正方形ABCD的面积;
(2)由正方形的边长为3可求得点D的坐标为(5,4),从而可求得直线OD的解析式,接下来求得OD与AB交点的坐标,从而可求得被分割的两部分的面积.
解答 解:(1)∵AB⊥x轴,
∴点A的横坐标为2.
将x=2代入得;y=2×2=4.
∴点A的坐标为(2,4).
∴AB=4-1=3.
∴正方形ABCD的面积=3×3=9.
(2)如图所示:记AB与OD的交点为E.
∵正方形的边长为3.
∴点D的坐标为(5,4).
设OD的解析式为y=kx,将(5,4)代入得:5k=4,
解得k=$\frac{4}{5}$.
∴直线OD的解析式为y=$\frac{4}{5}x$.
将x=2代入y=$\frac{4}{5}x$得:y=$\frac{8}{5}$.
∴AE=4-$\frac{8}{5}$=$\frac{12}{5}$,.
∴${S}_{△AED}=\frac{1}{2}×\frac{12}{5}×3$=$\frac{18}{5}$.
∴${S}_{EBCD}=9-\frac{18}{5}$=$\frac{27}{5}$.
∴S△AED:SEBCD=2:3.
点评 本题主要考查的是一次函数的图象和性质、正方形的性质、平行于坐标轴的直线上点的坐标特点,求得点A和点E的坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
| 销售方式 | 直接销售 | 加工成半成品 | 加工成成品 |
| 每方米获利(元) | 100 | 250 | 450 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{120}{x}=\frac{100}{x-10}$ | B. | $\frac{120}{x+10}=\frac{100}{x}$ | C. | $\frac{120}{x-10}=\frac{100}{x}$ | D. | $\frac{120}{x}=\frac{100}{x+10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
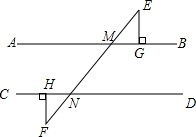 如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.
如图,直线EF和AB,CD分别相交于点M,N,EG⊥AB,FH⊥CD,垂足分别为G,H,且∠BME=53°,∠F=37°,试利用“三角形内角和等于180°”说明直线AB∥CD,EG∥FH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com