
分析 可设a+b=4t③,b+c=5t④,c+a=7t⑤,依此根据加减消元法用t表示出a,b,c,再代入②可求t,进一步求得a,b,c的值.
解答 解:$\left\{\begin{array}{l}{\frac{a+b}{4}=\frac{b+c}{5}=\frac{c+a}{7}①}\\{4a-c=3b+25②}\end{array}\right.$,
设a+b=4t③,b+c=5t④,c+a=7t⑤,
③-④得a-c=-t⑥,
⑤+⑥得2a=6t,
a=3t⑦,
则b=t⑧,c=4t⑨,
⑦⑧⑨代入②得12t-4t=3t+25,
解得t=5,
则a=3t=15,b=t=5,c=4t=20.
点评 考查了解三元一次方程组,解三元一次方程组的一般步骤:①首先利用代入法或加减法,把方程组中一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另外两个未知数的二元一次方程组.②然后解这个二元一次方程组,求出这两个未知数的值.③再把求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个关于第三个未知数的一元一次方程.④解这个一元一次方程,求出第三个未知数的值.⑤最后将求得的三个未知数的值用“{”合写在一起即可.


科目:初中数学 来源: 题型:解答题
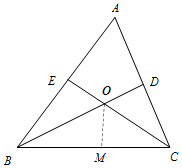 如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.
如图,△ABC中,∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 我爱美 | B. | 二中游 | C. | 爱我二中 | D. | 美我二中 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
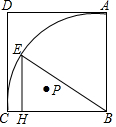 如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.
如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com