
方程 的解是( )
的解是( )
A. 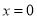 B.
B. 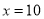 C.
C.  或
或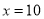 D.
D. 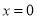 或
或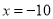
科目:初中数学 来源:北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型:解答题
先化简,再求值:  ,其中
,其中 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海口市八年级数学科期末检测模拟题(实验班卷) 题型:单选题
若x2-x+M=(x-4)·N,则M、N分别为( )
A. -12,x+3 B. 20,x-5 C. 12,x-3 D. -20,x+5
A 【解析】∵(x-4)(x+3)=x2+3x-4x-12=x2-x-12, ∴M=-12,N=x+3, 故选A查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:填空题
圆的内接四边形 ,已知
,已知 ,
, 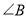 =__________ .
=__________ .
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2017-2018学年上学期九年级期末统一考试数学试卷 题型:单选题
如图,⊙ 与正方形
与正方形 的两边
的两边 相切,且
相切,且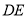 与⊙
与⊙ 相切于点
相切于点 .若
.若 ,
,  ,则⊙
,则⊙ 的半径为( )
的半径为( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年七年级上学期期末数学试卷 题型:解答题
已知关于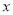 的方程
的方程 和
和 的解相同.
的解相同.
( )求
)求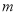 的值.
的值.
( )求式子
)求式子 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江杭州淳安2016-2017学年七年级上学期期末数学试卷 题型:填空题
求 的平方根与
的平方根与 的立方根的和是__________.
的立方根的和是__________.
查看答案和解析>>
科目:初中数学 来源:广西柳州市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在长为20cm,宽为16cm的矩形的四个角上截去四个全等的小正方形,使得剩下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去的小正方形的边长.

查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试八年级数学试卷 题型:解答题
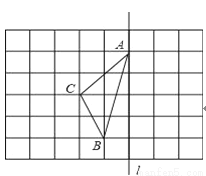
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′;
(2)求△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com