Question

问题探究．
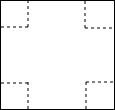
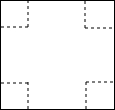
用如图所示正方形纸板制作一个无盖的长方体盒子，可在正方体的四角减去相同的正方形，剩余部分即可做成一个无盖的长方体形盒子．
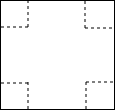
（1）设正方形纸的边长为a，减去的小正方形的边长为x，请用a与x表示这个无盖长方体形盒子的容积；
（2）把正方形的纸板换成长为a，宽为b的长方形纸板，怎样做一个无盖长方体形盒子？画图说明你的做法；
（3）把（2）中做的长方体形盒子的容积用代数式表示出来；
（4）比较（1）和（3）的结果，说说它们的区别和联系．

Answer 1

解：（1）依题意，长方体盒子容积为：（a-2x）²•x；

（2）画图如下：

（3）设减去的正方形边长为x，根据题意得：
（a-2x）（b-2x）•x；

（4）（1）中底面积为正方形面积为（a-2x）²，（3）中底面积为长方形，面积为（a-2x）（b-2x），高都为x，（3）中当a=b时即得到（1）中的结果．
分析：（1）观察图形可知底面长、宽都为（a-2x），高为x，用长方体的体积公式表示体积；
（2）在长方形纸板的四个角减去相同的正方形，剩余部分即可做成一个无盖的长方体形盒子；
（3）先设减去的正方形边长为x，然后求出长方体盒子的底面积，再乘以高即可得出答案；
（4）根据长方体和正方体的体积公式即可得出它们之间的区别和联系．
点评：此题考查了列代数式；本题关键是表示长方体的长、宽、高，再用体积公式计算．