
【题目】已知二次函数y=![]() x2+bx的图象过点A(4,0),设点C(1,-3),在抛物线的对称轴上求一点P,使|PA-PC|的值最大,则点P的坐标为____________。
x2+bx的图象过点A(4,0),设点C(1,-3),在抛物线的对称轴上求一点P,使|PA-PC|的值最大,则点P的坐标为____________。
【答案】(2,-6)
【解析】
先把A(4,0)代入y=![]() x2+bx,求出b的值,得到二次函数解析式,再根据抛物线的对称性求出二次函数y=
x2+bx,求出b的值,得到二次函数解析式,再根据抛物线的对称性求出二次函数y=![]() x2-2x与x轴的另一交点是O(0,0),由A、O关于对称轴对称,则可知PA=PO,则当P、O、C三点在一条线上时满足|PA-PC|最大,利用待定系数法可求得直线OC解析式,则可求得P点坐标.
x2-2x与x轴的另一交点是O(0,0),由A、O关于对称轴对称,则可知PA=PO,则当P、O、C三点在一条线上时满足|PA-PC|最大,利用待定系数法可求得直线OC解析式,则可求得P点坐标.
∵二次函数y=![]() x2+bx的图象过点A(4,0),
x2+bx的图象过点A(4,0),
∴0=![]() ×42+4b,解得b=-2,
×42+4b,解得b=-2,
∴y=![]() x2-2x,
x2-2x,
∴对称轴为x=![]() =2,
=2,
∵二次函数y=![]() x2-2x与x轴交于点A(4,0),
x2-2x与x轴交于点A(4,0),
∴它与x轴的另一交点是O(0,0),
∵P在对称轴上,
∴PA=PO,
∴|PA-PC|=|PO-PC|≤OC,即当P、O、C三点在一条线上时|PA-PC|的值最大,
设直线OC解析式为y=kx,
∴k=-3,
∴直线OC解析式为y=-3x,
令x=2,可得y=-3×2=-6,
∴存在满足条件的点P,其坐标为(2,-6).
故答案为(2,-6).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,两车分别从路段AB两端同时出发,沿平行路线AC、BD行驶,CE和DF的长分别表示两车到道路AB的距离.

(1)求证:△ACE∽△BDF;
(2)如果两车行驶速度相同,求证:△ACE≌△BDF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一片等边三角形形状的草地,为方便人们休闲,现决定在草地内部修建一座小亭,小亭离三个出口即三角形三个顶点A、B、C的距离相等.

(1)用尺规作图的方法确定小亭的位置.
(2)若草地的边长50m,求小亭到出口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
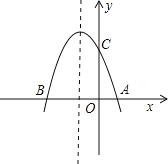
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是⊙O的直径,弦BC与OA相交于点E,AF与⊙O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.
(1)求∠ADB的度数;
(2)求AC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰梯形ABCD中,AD∥BC,AD=3,AB=CD=4,BC=5,∠B的平分线交DC于点E,交AD的延长线于点F.
(1)如图(1),若∠C的平分线交BE于点G,写出图中所有的相似三角形(不必证明);
(2)在(1)的条件下求BG的长;
(3)若点P为BE上动点,以点P为圆心,BP为半径的⊙P与线段BC交于点Q(如图(2)),请直接写出当BP取什么范围内值时,①点A在⊙P内;②点A在⊙P内而点E在⊙P外.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
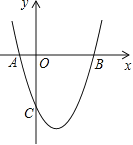
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣mx﹣3x+m﹣4=0(m为常数)
(1)求证:方程有两个不相等的实数根.
(2)设x1,x2是方程的两个实数根,且x1+x2=4,请求出方程的这两个实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com