
分析 (1)因为都是8个相同的正方体拼成的,所以体积相等,根据“正方体的体积=棱长3”求出一个正方体的体积,然后乘8解答即可;
(2)表面积不等:①8×1×1拼法;②4×2×1拼法; ③2×2×2拼法(特殊的长方体,即正方体);分别计算即可.
解答 解:(1)体积都相等,都为:10×10×10×8=8000cm3;
(2)①8×1×1拼法:
10×8=80(厘米),
(80×10+80×10+10×10)×2,
=1700×2,
=3400(平方厘米);
②4×2×1拼法:
长是4×10=40(厘米),宽是10×2=20(厘米),
(40×20+40×10+20×10)×2,
=1400×2,
=2800(平方厘米);
③2×2×2拼法:
10×2=20(厘米),
(20×20)×6,
=400×6,
=2400(平方厘米);
答:(1)不同的拼法得出的长方体的体积是相等的,都是8000cm3;
(2)有3种不同的拼法,所拼成的长方体的表面积分别是3400cm2,2800cm2,2400cm2.
点评 本题考查了几何体的表面积,解答此题应根据长方体的表面积和体积计算方法,进行解答即可.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
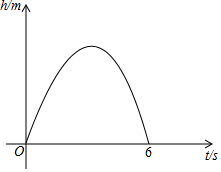 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
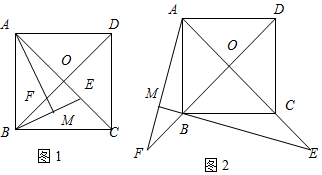 如图1,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.
如图1,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
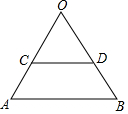 如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG
如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com