
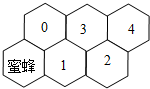
 10、假定有一排蜂房,形状如图,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去.则从最初位置爬到4号蜂房中,不同的爬法有( )
10、假定有一排蜂房,形状如图,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去.则从最初位置爬到4号蜂房中,不同的爬法有( )科目:初中数学 来源: 题型:
 15、假定有一排蜂房,形状如图,一只蜜峰在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,蜜蜂爬到1号蜂房的爬法有:蜜蜂→1号;蜜蜂→0号→1号共有2种不同的爬法,若蜜蜂从最初位置爬到4号蜂房共有n种不同爬法,则n等于
15、假定有一排蜂房,形状如图,一只蜜峰在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,蜜蜂爬到1号蜂房的爬法有:蜜蜂→1号;蜜蜂→0号→1号共有2种不同的爬法,若蜜蜂从最初位置爬到4号蜂房共有n种不同爬法,则n等于查看答案和解析>>
科目:初中数学 来源: 题型:
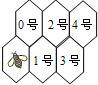 8、假定有一排蜂房,形状如图,一只蜜蜂在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,密封爬到1号蜂房的爬法有:蜜蜂?1号;蜜蜂?0号?1号,共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有几种不同的爬法( )
8、假定有一排蜂房,形状如图,一只蜜蜂在左下角,由于受了点伤,只能爬行,不能飞,而且始终向右方(包括右上、右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如,密封爬到1号蜂房的爬法有:蜜蜂?1号;蜜蜂?0号?1号,共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有几种不同的爬法( )查看答案和解析>>
科目:初中数学 来源: 题型:
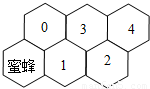
 假定有一排蜂房,形状如图,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去,则从最初位置爬到4号蜂房中,不同的爬法有
假定有一排蜂房,形状如图,一只蜜蜂在左下角的蜂房中,由于受伤,只能爬,不能飞,而且只能永远向右方(包括右上、右下)爬行,从一间蜂房爬到与之相邻的右蜂房中去,则从最初位置爬到4号蜂房中,不同的爬法有查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市建兰中学中考数学模拟试卷(二)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com