
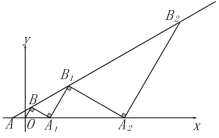
【题目】在直角坐标系中,如图所示,把∠BAO放在直角坐标系中,使射线AO与x轴重合,已知BAO=30°,OA=OB=1,过点B作BA1⊥OB交x轴于A1,过点A1做B1A1⊥BA1交直线AB于点B1,过B1作B1A2⊥B1A1交x轴于点A2,再过A2依次作垂直….则△A6B6A7的面积为_____.
【答案】![]() .
.
【解析】
根据OA的长即可求出A的坐标,根据OB和∠BOA1=60°,即可求出B的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入得出方程组,求出方程组的解;推出∠BAC=∠ABO=30°,求出∠BOC=60°,∠BA1O=30°,求出BA1=![]() ,求出A1B1=
,求出A1B1=![]() ×
×![]() 、B1A2=3
、B1A2=3![]() =
=![]() ×
×![]() ×
×![]() ,同理求出A6B6=12个
,同理求出A6B6=12个![]() 相乘,B6A7=13个
相乘,B6A7=13个![]() 相乘,根据三角形的面积公式求出即可.
相乘,根据三角形的面积公式求出即可.
∵OA=1,
∴A(-1,0),
易求B(![]() ,
,![]() ).
).
设直线AB的解析式是:y=kx+b,
把A(-1,0),B(![]() ,
,![]() )代入得:
)代入得:
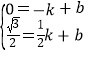 ,
,
解得: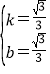 ,
,
∴直线AB的解析式为:y=![]() x+
x+![]() .
.
∵OB=OA=1,
∴∠BAC=∠ABO=30°,
∴∠BOC=60°,
∴∠BA1O=30°,
∴BA1=![]() ,
,
同理∠BB1A1=30°,
∴B1A1=3=![]() ×
×![]() ,
,
同理:B1A2=3![]() =
=![]() ×
×![]() ×
×![]() ,
,
…
A6B6=![]() ×
×![]() ×…×
×…×![]() (12个
(12个![]() 相乘),
相乘),
B6A7=![]() ×
×![]() ×…×
×…×![]() (13个
(13个![]() 相乘),
相乘),
∴△A6B6A7的面积是:![]() A6B6×B6A7=
A6B6×B6A7=![]() ×(
×(![]() ×
×![]() ×…×
×…×![]() )×(
)×(![]() ×
×![]() ×…×
×…×![]() )
)
=![]() ,
,
答:△A6B6A7的面积是![]() .
.


科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点.
为平面内一点.
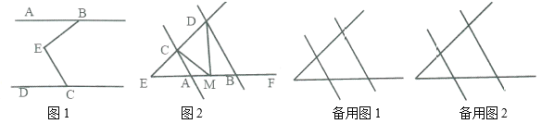
(1)如图1,![]() 和
和![]() 互余,小明说过
互余,小明说过![]() 作
作![]() ,很容易说明
,很容易说明![]() 。请帮小明写出具体过程;
。请帮小明写出具体过程;
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上移动时(点
上移动时(点![]() 与
与![]() ,
,![]() 两点不重合),指出
两点不重合),指出![]() 与
与![]() ,
,![]() 的数量关系?请说明理由;
的数量关系?请说明理由;
(3)在(2)的条件下,若点![]() 在
在![]() ,
,![]() 两点外侧运动(点
两点外侧运动(点![]() 与
与![]() ,
,![]() ,
,![]() 三点不重合)请直接写出
三点不重合)请直接写出![]() 与
与![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
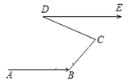
【题目】“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经 B,C,D 三点拐弯后与原来流向相同,若∠ABC =6∠CDE,∠BCD =4∠CDE,则∠CDE= _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD的纸片中,AC⊥AB,AC与BD交于O,将△ABC沿对角线AC翻折得到![]() .
.
(1)求证:四边形ACDB’是矩形.
(2)若平行四边形ABCD的面积为12,求翻折后纸片重叠部分的面积,即![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0)、B(3,0).抛物线y=x2﹣2mx+m2﹣4的顶点为P,与y轴的交点为Q.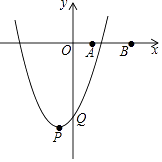
(1)填空:点P的坐标为;点Q的坐标为(均用含m的代数式表示)
(2)当抛物线经过点A时,求点Q的坐标.
(3)连接QA、QB,设△QAB的面积为S,当抛物线与线段AB有公共点时,求S与m之间的函数关系式.
(4)点P、Q不重合时,以PQ为边作正方形PQMN(P、Q、M、N分别按顺时针方向排列).当正方形PQMN的四个顶点中,位于x轴两侧或y轴两侧的顶点个数相同时,直接写出此时m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
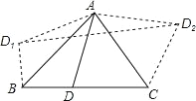
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】相传,大禹治水时,洛水中出现了一个“神龟”背上有美妙的图案,史称“洛书”,用现在的数字翻译出来,就是三阶幻方.三阶幻方是最简单的幻方,又叫九宫格,它是由九个数字组成的一个三行三列的矩阵.其对角线、横行、纵向的数字之和均相等,这个和叫做幻和,正中间那个数叫中心数,如图(1)是由![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所组成的一个三阶幻方,其幻和为
所组成的一个三阶幻方,其幻和为![]() ,中心数为
,中心数为![]() .如图(2)是一个新三阶幻方,该新三阶幻方的幻和为
.如图(2)是一个新三阶幻方,该新三阶幻方的幻和为![]() 的
的![]() 倍,且
倍,且![]() ,则
,则![]() _______.
_______.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖为妈妈准备了一份生日礼物,礼物外包装盒为长方体形状,长、宽、高分别为![]() 、
、![]() 、
、![]()
![]() ,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为
,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为![]() ,
,![]() ,
,![]() (不计打结处丝带长度)
(不计打结处丝带长度)

(1)用含![]() 、
、![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() ,
,![]() ;
;
(2)方法简介:
要比较两数![]() 与
与![]() 大小,我们可以将
大小,我们可以将![]() 与
与![]() 作差,结果可能出现三种情况:
作差,结果可能出现三种情况:
①![]() ,则
,则![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() ,则
,则![]() ;
;
我们将这种比较大小的方法叫做“作差法”.
请帮小颖选出最节省丝带的打包方式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: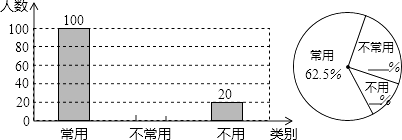
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com