
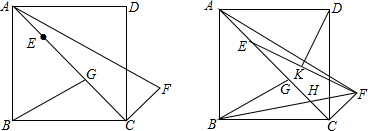
分析 (1)连接BD,利用两边对应成比例且夹角相等证明△ACF∽△BOG,得∠AFC=∠AGB;
(2)连接对角线BD,得直角△EOM和直角△BOG,设OG=x,利用平行成比例性质表示出边FC、BO、GH、OM、DM的长,再利用三角函数表示出DK的长,最后计算$\frac{DK}{GH}$的值,得出结论.
解答 证明:(1)如图1,连接BD交AC于点O,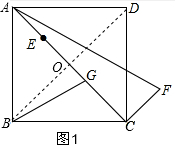
∵四边形ABCD是正方形,
∴AO=BO=CO=$\frac{1}{2}$AC,∠BOC=90°,$\frac{AC}{OB}=\frac{2}{1}$,
∵∠ACF=90°,
∴∠BOC=∠ACF,
∵EG=CG,
∴AO-EG=CO-CG=OG,
∵AO-EG=AE+EO-(OE+OG)=AE-OG,
∴AE-OG=OG,
∴AE=2OG,
∴CF=AE=2OG,
∴$\frac{CF}{OG}=\frac{2}{1}$,
∴$\frac{AC}{OB}=\frac{CF}{OG}$,
∴△ACF∽△BOG,
∴∠AFC=∠AGB;
(2)如图2,DK=$\frac{3\sqrt{10}}{5}$GH,理由是:
连接BD交AC于O,交EF于M,
设OG=x,则FC=2x,
∵OB∥FC,
∴$\frac{BH}{HF}=\frac{OB}{FC}=\frac{OH}{HC}=\frac{2}{1}$,
∴OB=2FC=4x,OH=2HC,
则GH=OH-OG=$\frac{8x}{3}$-x=$\frac{5x}{3}$,OE=OA-AE=4x-2x=2x,
∵OM∥FC,
∴$\frac{OM}{FC}=\frac{OE}{EC}$,
∴$\frac{OM}{2x}=\frac{2x}{2x+4x}$,
∴OM=$\frac{2X}{3}$,
由勾股定理得:EM=$\sqrt{(2x)^{2}+(\frac{2x}{3})^{2}}$=$\frac{2\sqrt{10}x}{3}$,
则DM=4x-$\frac{2x}{3}$=$\frac{10x}{3}$,
在△EOM和△DKM中,∠EOM=∠MKD,∠EMO=∠KMD,
∴∠CEF=∠MDK,
∵cos∠CEF=$\frac{OE}{EM}$,cos∠MDK=$\frac{DK}{DM}$,
∴$\frac{OE}{EM}=\frac{DK}{DM}$,
∴$\frac{2x}{\frac{2\sqrt{10}x}{3}}$=$\frac{DK}{\frac{10x}{3}}$,
∴DK=$\sqrt{10}x$,
∴$\frac{DK}{GH}$=$\frac{\sqrt{10}x}{\frac{5x}{3}}$=$\frac{3\sqrt{10}}{5}$,
则DK=$\frac{3\sqrt{10}}{5}$GH.
点评 本题是四边形的综合题,考查了正方形和平行线截线段成比例的性质,在几何证明中,如果不能求边的具体长度,可以设某一小边为x,利用比例式表示一些线段的长,最后得出结论;同时可以利用同角的三角函数值来求边的长度,比利用勾股定理要简单.


科目:初中数学 来源:2016-2017学年山东省淄博市(五四学制)七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下面有3个命题:①同旁内角互补;②两直线平行,内错角相等;③垂直于同一条直线的两直线互相平行.其中真命题为 ( )
A. ① B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省东台市第六教育联盟七年级下学期第一次月考数学试卷 题型:选择题
已知∠1与∠2是同位角,若∠1=40°,则∠2的度数是( )
A.40° B.140° C.40°或140° D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线CD与直线AB相交于C,
如图,直线CD与直线AB相交于C,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 本次调查属于普查 | B. | 每名考生的中考体育成绩是个体 | ||
| C. | 550名考生是总体的一个样本 | D. | 2198名考生是总体 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com