
【题目】如图,等腰△ABC如图放置,顶角的顶点C在直线m上,分别过点A、B作直线m的垂线,垂足分别为E、D,且AE=CD.
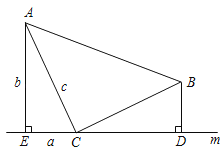
(1)求证:△AEC≌△CDB;
(2)若设△AEC的三边长分別为a、b、c,利用此图证明勾股定理.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A坐标为(﹣2![]() ,0),∠OAB=90°,∠AOB=30°,将△OAB绕点O按顺时针方向旋转,旋转角为α(0°<α≤150°),在旋转过程中,点A、B的对应点分别为点A′、B′.
,0),∠OAB=90°,∠AOB=30°,将△OAB绕点O按顺时针方向旋转,旋转角为α(0°<α≤150°),在旋转过程中,点A、B的对应点分别为点A′、B′.
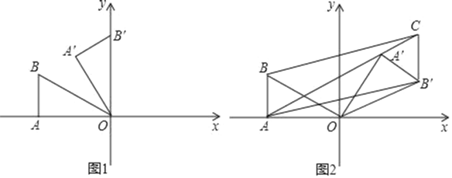
(1)如图1,当α=60°时,直接写出点A′ 、B′ 的坐标;
(2)如图2,当α=135°时,过点B′作AB的平行线交AA′延长线于点C,连接BC,AB′.
①判断四边形AB′CB的形状,并说明理由,
②求此时点A′和点B′的坐标;
(3)当α由30°旋转到150°时,(2)中的线段B′C也随之移动,请求出B′C所扫过的区域的面积?(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
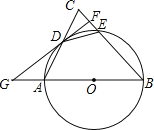
【题目】如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.
(1)求证:BA=BC;
(2)若AG=2,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
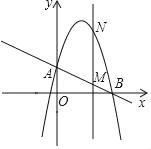
【题目】如图,已知抛物线y=﹣x2+bx+c(b,c是常数)经过A(0,2)、B(4,0)两点.
(1)求该抛物线的解析式和顶点坐标;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这条抛物线于N,求当t取何值时,MN有最大值?最大值是多少?
(3)在(1)的情况下,以A、M、N、D为顶点作平行四边形,请直接写出第四个顶点D的所有坐标(直接写出结果,不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
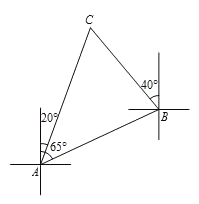
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
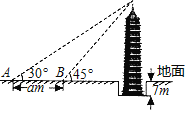
【题目】荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为_____米(![]() ≈1.73,结果精确到0.1).
≈1.73,结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象
)的图象![]() 经过点
经过点![]() (4,1),直线
(4,1),直线![]() 与图象
与图象![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有4个整点,结合函数图象,求
内恰有4个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com