
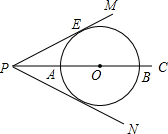
 如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.分析 (1)连接OE,过O作OF⊥PN,根据角平分线的性质定理可得OF=OE,即可确定出PN与圆O相切;
(2)在直角三角形POE中,利用30度所对的直角边等于斜边的一半求出OE的长,∠EOB度数,利用弧长公式即可求出劣弧$\widehat{BE}$的长.
解答  (1)证明:连接OE,过O作OF⊥PN,如图所示,
(1)证明:连接OE,过O作OF⊥PN,如图所示,
∵PM与圆O相切,
∴OE⊥PM,
∴∠OEP=∠OFP=90°,
∵PC平分∠MPN,
∴OF=OE,
则PN与圆O相切;
(2)在Rt△EPO中,∠MPC=30°,PE=2$\sqrt{3}$,
∴∠EOP=60°,OE=2,
∴∠EOB=120°,
则$\widehat{BE}$的长l=$\frac{120π×2}{180}$=$\frac{4π}{3}$.
点评 此题考查了切线的判定与性质,弧长公式,熟练掌握切线的判定与性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
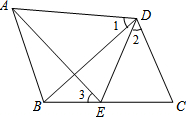 已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.
已知:如图,AD=BD,CD=ED,∠1=∠2,试说明∠3=∠1的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (31,50) | B. | (32,47) | C. | (33,46) | D. | (34,42) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
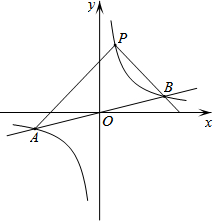 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
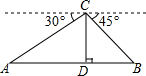 4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200$\sqrt{3}$+200米.
4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200$\sqrt{3}$+200米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com