
”¾ĢāÄæ”æŅ»æģµŻŌ±ŠčŅŖŌŚ¹ę¶ØŹ±¼äÄŚæŖ³µ½«æģµŻĖĶµ½Ä³µŲ£¬ČōæģµŻŌ±æŖ³µĆæ·ÖÖÓŠŠŹ»1.2![]() £¬¾ĶŌēµ½10·ÖÖÓ£»ČōæģµŻŌ±æŖ³µĆæ·ÖÖÓŠŠŹ»0.8
£¬¾ĶŌēµ½10·ÖÖÓ£»ČōæģµŻŌ±æŖ³µĆæ·ÖÖÓŠŠŹ»0.8![]() £¬¾ĶŅŖ³Łµ½5·ÖÖÓ.ŹŌĒó³ö¹ę¶ØŹ±¼ä¼°æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³Ģ.
£¬¾ĶŅŖ³Łµ½5·ÖÖÓ.ŹŌĒó³ö¹ę¶ØŹ±¼ä¼°æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³Ģ.
Š”Ć÷ŗĶŠ”ŠĀŌŚ½ā“šŹ±ĻČÉč³öĪ“ÖŖŹż£¬Č»ŗóĮŠ³ö·½³ĢČēĻĀ£ŗ
![]() ¢Ł£¬
¢Ł£¬![]() ¢Ś£¬ĘäÖŠ·½³Ģ¢ŁÓÉŠ”Ć÷ĖłĮŠ£¬·½³Ģ¢ŚÓÉŠ”ŠĀĖłĮŠ.
¢Ś£¬ĘäÖŠ·½³Ģ¢ŁÓÉŠ”Ć÷ĖłĮŠ£¬·½³Ģ¢ŚÓÉŠ”ŠĀĖłĮŠ.
£Ø1£©Š”Ć÷ĖłÉč![]() ±ķŹ¾ £»
±ķŹ¾ £»
Š”ŠĀĖłÉč![]() ±ķŹ¾ .
±ķŹ¾ .
£Ø2£©ĒėŃ”Š”Ć÷»ņŠ”ŠĀµÄ·½·ØŠ“³öĶźÕūµÄ½ā“š¹ż³Ģ.
”¾“š°ø”æ£Ø1£©¹ę¶ØŹ±¼ä£»æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³Ģ£»£Ø2£©Š“³öĶźÕūµÄ½ā“š¹ż³Ģ¼ū½āĪö.
”¾½āĪö”æ
£Ø1£©Š”Ć÷ŹĒøł¾ŻŠŠŹ»µÄ×ÜĀ·³ĢĻąµČĮŠŹ½£¬¹ŹĖłÉčx±ķŹ¾¹ę¶ØŹ±¼ä£»Š”ŠĀøł¾Ż¹ę¶ØŹ±¼äĻąĶ¬ĮŠŹ½£¬¹ŹĖłÉčx±ķŹ¾æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³Ģ.
£Ø2£©øł¾Ż£Ø1£©ÖŠµÄ·ÖĪö£¬Ń”Č”Š”Ć÷»ņŠ”ŠĀµÄ·½·Ø£¬Éč³öĪ“ÖŖŹż£¬ĮŠ·½³Ģ£¬½ā·½³Ģ¼“æÉ.
£Ø1£©Š”Ć÷ŹĒøł¾ŻŠŠŹ»µÄ×ÜĀ·³ĢĻąµČĮŠŹ½£¬¹ŹĖłÉčx±ķŹ¾¹ę¶ØŹ±¼ä£»Š”ŠĀøł¾Ż¹ę¶ØŹ±¼äĻąĶ¬ĮŠŹ½£¬¹ŹĖłÉčx±ķŹ¾æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³Ģ.
¹Ź“š°øĪŖ£ŗ¹ę¶ØŹ±¼ä£»æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³Ģ.
£Ø2£©Š”Ć÷µÄ·½·Ø£ŗÉč¹ę¶ØŹ±¼äĪŖ![]() ·ÖÖÓ£¬
·ÖÖÓ£¬
øł¾ŻĢāŅāµĆ£ŗ![]() £¬½āÖ®µĆ
£¬½āÖ®µĆ![]() £¬
£¬
![]() £Ø
£Ø![]() £©
£©
“š£ŗ¹ę¶ØŹ±¼äĪŖ40·ÖÖÓ£¬æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³ĢĪŖ36![]() .
.
Š”ŠĀµÄ·½·Ø£ŗÉčæģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³ĢĪŖ![]()
![]() £¬
£¬
øł¾ŻĢāŅāµĆ£ŗ![]()
½āÖ®µĆx=36
![]() +10=40£Ø·ÖÖÓ£©
+10=40£Ø·ÖÖÓ£©
“š£ŗ¹ę¶ØŹ±¼äĪŖ40·ÖÖÓ£¬æģµŻŌ±ĖłŠŠŹ»µÄ×ÜĀ·³ĢĪŖ36![]() .
.


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
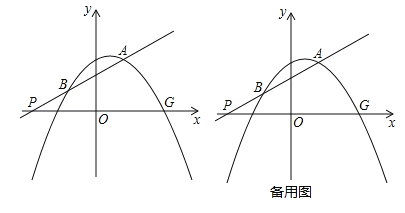
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=©![]() x2+mx+nµÄĶ¼Ļó¾¹żµćA£Ø2£¬3£©£¬ÓėxÖįµÄÕż°ėÖį½»ÓŚµćG£Ø1+
x2+mx+nµÄĶ¼Ļó¾¹żµćA£Ø2£¬3£©£¬ÓėxÖįµÄÕż°ėÖį½»ÓŚµćG£Ø1+![]() £¬0£©£»Ņ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó¾¹żµćA£¬ĒŅ½»xÖįÓŚµćP£¬½»Å×ĪļĻßÓŚĮķŅ»µćB£¬ÓÖÖŖµćA£¬BĪ»ÓŚµćPµÄĶ¬²ą£®
£¬0£©£»Ņ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó¾¹żµćA£¬ĒŅ½»xÖįÓŚµćP£¬½»Å×ĪļĻßÓŚĮķŅ»µćB£¬ÓÖÖŖµćA£¬BĪ»ÓŚµćPµÄĶ¬²ą£®
£Ø1£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ČōPA=3PB£¬ĒóŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±k£¾0Ź±£¬Å×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚµćC£¬Ź¹”ŃCĶ¬Ź±ÓėxÖįŗĶÖ±ĻßAP¶¼ĻąĒŠ£æČē¹ū“ęŌŚ£¬ĒėĒó³öµćCµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹży=k1x+bµÄĶ¼Ļó·Ö±šÓėxÖį”¢yÖįµÄÕż°ėÖį½»ÓŚ A£¬B Į½µć£¬ĒŅÓė·“±ČĄżŗÆŹży=![]() ½»ÓŚ C£¬E Į½µć£¬µć C ŌŚµŚ¶žĻóĻŽ£¬¹żµć C ×÷CD”ĶxÖįÓŚµć D£¬AC=2
½»ÓŚ C£¬E Į½µć£¬µć C ŌŚµŚ¶žĻóĻŽ£¬¹żµć C ×÷CD”ĶxÖįÓŚµć D£¬AC=2![]() £¬OA=OB=1£®
£¬OA=OB=1£®

£Ø1£©”÷ADC µÄĆ껿£»
£Ø2£©Ē󷓱ȥżŗÆŹży= ![]() ÓėŅ»“ĪŗÆŹżµÄy=k1x+b±ķ“ļŹ½£®
ÓėŅ»“ĪŗÆŹżµÄy=k1x+b±ķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖM£½£Øa£«24£©x3©10x2£«10x£«5ŹĒ¹ŲÓŚxµÄ¶ž“Ī¶ąĻīŹ½£¬ĒŅ¶ž“ĪĻīĻµŹżŗĶŅ»“ĪĻīĻµŹż·Ö±šĪŖbŗĶc£¬ŌŚŹżÖįÉĻA”¢B”¢CČżµćĖł¶ŌÓ¦µÄŹż·Ö±šŹĒa”¢b”¢c£®
![]()
£Ø1£©Ōņa£½ £¬b£½ £¬c£½ £®
£Ø2£©ÓŠŅ»¶ÆµćP“ÓµćA³ö·¢£¬ŅŌĆæĆė4øöµ„Ī»µÄĖŁ¶ČĻņÓŅŌĖ¶Æ£¬¶ąÉŁĆėŗó£¬Pµ½A”¢B”¢CµÄ¾ąĄėŗĶĪŖ40øöµ„Ī»£æ
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±µćPŅĘ¶Æµ½µćBŹ±Į¢¼“µōĶ·£¬ĖŁ¶Č²»±ä£¬Ķ¬Ź±µćTŗĶµćQ·Ö±š“ÓµćAŗĶµćC³ö·¢£¬Ļņ×óŌĖ¶Æ£¬µćTµÄĖŁ¶Č1øöµ„Ī»/Ćė£¬µćQµÄĖŁ¶Č5øöµ„Ī»/Ćė£¬ÉčµćP”¢Q”¢TĖł¶ŌÓ¦µÄŹż·Ö±šŹĒxP”¢xQ”¢xT£¬µćQ³ö·¢µÄŹ±¼äĪŖt£¬µ±![]() £¼t£¼
£¼t£¼![]() Ź±£¬Ēó2|xP©xT|£«|xT©xQ|£«2|xQ©xP|µÄÖµ£®
Ź±£¬Ēó2|xP©xT|£«|xT©xQ|£«2|xQ©xP|µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDŹĒÖį¶Ō³ĘĶ¼ŠĪ£¬ĒŅÖ±ĻßACŹĒ·ń¶Ō³ĘÖį£¬AB”ĪCD£¬ŌņĻĀĮŠ½įĀŪ£ŗ¢ŁAC”ĶBD£»¢ŚAD”ĪBC£»¢ŪĖıߊĪABCDŹĒĮāŠĪ£»¢Ü”÷ABD”Õ”÷CDB£®ĘäÖŠ½įĀŪÕżČ·µÄŠņŗÅŹĒ£Ø””””£©

A. ¢Ł¢Ś¢Ū B. ¢Ł¢Ś¢Ū¢Ü C. ¢Ś¢Ū¢Ü D. ¢Ł¢Ū¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹży=![]() x2+
x2+![]() x©
x©![]() µÄĶ¼ĻóÓėxÖį½»ÓŚµć A£¬B£¬½» y ÖįÓŚµć C£¬Å×ĪļĻߵĶ„µćĪŖ D£®
µÄĶ¼ĻóÓėxÖį½»ÓŚµć A£¬B£¬½» y ÖįÓŚµć C£¬Å×ĪļĻߵĶ„µćĪŖ D£®
£Ø1£©ĒóÅ×ĪļĻ߶„µć D µÄ×ų±źŅŌ¼°Ö±Ļß AC µÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©µć P ŹĒÅ×ĪļĻßÉĻŅ»µć£¬ĒŅµćPŌŚÖ±Ļß AC ĻĀ·½£¬µć E ŌŚÅ×ĪļĻ߶Ō³ĘÖįÉĻ£¬µ±”÷BCE µÄÖܳ¤×īŠ”Ź±£¬Ēó”÷PCE Ć껿µÄ×ī“óÖµŅŌ¼°“ĖŹ±µć P µÄ×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬¹żµć P ĒŅĘ½ŠŠÓŚ AC µÄÖ±Ļß·Ö±š½»xÖįÓŚµć M£¬½» y ÖįÓŚµćN£¬°ŃÅ×ĪļĻßy=![]() x2+
x2+![]() x©
x©![]() ŃŲ¶Ō³ĘÖįÉĻĻĀĘ½ŅĘ£¬Ę½ŅĘŗóÅ×ĪļĻߵĶ„µćĪŖ D'£¬ŌŚĘ½ŅĘµÄ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚµć D'£¬Ź¹µĆµć D'£¬M£¬N Čżµć¹¹³ÉµÄČż½ĒŠĪĪŖÖ±½ĒČż½ĒŠĪ£¬Čō“ęŌŚ£¬Ö±½ÓŠ“³öµć D'µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
ŃŲ¶Ō³ĘÖįÉĻĻĀĘ½ŅĘ£¬Ę½ŅĘŗóÅ×ĪļĻߵĶ„µćĪŖ D'£¬ŌŚĘ½ŅĘµÄ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚµć D'£¬Ź¹µĆµć D'£¬M£¬N Čżµć¹¹³ÉµÄČż½ĒŠĪĪŖÖ±½ĒČż½ĒŠĪ£¬Čō“ęŌŚ£¬Ö±½ÓŠ“³öµć D'µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚČĪŅāĮ½øöŹµŹż¶Ō£Øa£¬b£©ŗĶ£Øc£¬d£©£¬¹ę¶Ø£ŗµ±ĒŅ½öµ±a£½cĒŅb£½dŹ±£¬ £Øa£¬b£©£½£Øc£¬d£©£®¶ØŅåŌĖĖć”°![]() ”±£ŗ£Øa£¬b£©
”±£ŗ£Øa£¬b£©![]() £Øc£¬d£©£½£Øac£bd£¬ad£«bc£©£®Čō£Ø1£¬2£©
£Øc£¬d£©£½£Øac£bd£¬ad£«bc£©£®Čō£Ø1£¬2£©![]() £Øp£¬3£©£½£Øq£¬q£©£¬Ōņpq£½___________£®
£Øp£¬3£©£½£Øq£¬q£©£¬Ōņpq£½___________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(1)°ŃŹżÖį²¹³äĶźÕū.
(2)ŌŚŹżÖįÉĻ±ķŹ¾ĻĀĮŠø÷Źż£ŗ3![]() £¬©4£¬©(©1.5)£¬©|©2|.
£¬©4£¬©(©1.5)£¬©|©2|.
(3)ÓĆ”°£¼”±Į¬½ÓĘšĄ“._____________
(4)©|©2|Óė©4Ö®¼äµÄ¾ąĄėŹĒ_________.
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ½ā¾öŹżŃ§ĪŹĢāµÄ¹ż³ĢÖŠ£¬ĪŅĆĒ³£ÓƵ½”°·ÖĄąĢÖĀŪ”±µÄŹżŃ§Ė¼Ļė£¬ĻĀĆęŹĒŌĖÓĆ·ÖĄąĢÖĀŪµÄŹżŃ§Ė¼Ļė½ā¾öĪŹĢāµÄ¹ż³Ģ£¬Ēė׊ĻøŌĶĮ£¬²¢½ā“šĪŹĢā.
£ØĢį³öĪŹĢā£©ČżøöÓŠĄķŹż![]() ”¢
Ӣ![]() Ӣ
”¢![]() Āś×ć
Āś×ć![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
£Ø½ā¾öĪŹĢā£©
½ā£ŗÓÉĢāŅā£¬µĆ![]() ”¢
Ӣ![]() Ӣ
”¢![]() ČżøöÓŠĄķŹż¶¼ĪŖÕżŹż»ņĘäÖŠŅ»øöĪŖÕżŹż£¬ĮķĮ½øöĪŖøŗŹż£¬
ČżøöÓŠĄķŹż¶¼ĪŖÕżŹż»ņĘäÖŠŅ»øöĪŖÕżŹż£¬ĮķĮ½øöĪŖøŗŹż£¬
¢Ł![]() ”¢
Ӣ![]() Ӣ
”¢![]() ¶¼ŹĒÕżŹż£¬¼“
¶¼ŹĒÕżŹż£¬¼“![]() ”¢
Ӣ![]() Ӣ
”¢![]() Ź±£¬Ōņ
Ź±£¬Ōņ![]() £ŗ
£ŗ
¢Śµ±![]() ”¢
Ӣ![]() Ӣ
”¢![]() ÖŠÓŠŅ»øöĪŖÕżŹż£¬ĮķĮ½øöĪŖøŗŹżŹ±£¬²»·ĮÉč
ÖŠÓŠŅ»øöĪŖÕżŹż£¬ĮķĮ½øöĪŖøŗŹżŹ±£¬²»·ĮÉč![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬Ōņ£¬
£¬Ōņ£¬![]() £¬×ŪÉĻĖłŹö£¬
£¬×ŪÉĻĖłŹö£¬![]() ÖµĪŖ
ÖµĪŖ![]() »ņ
»ņ![]() .
.
£ØĢ½¾æ£©Ēėøł¾ŻÉĻĆęµÄ½āĢāĖ¼Ā·½ā“šĻĀĆęµÄĪŹĢā£ŗ
£Ø1£©ČżøöÓŠĄķŹż![]() ”¢
Ӣ![]() Ӣ
”¢![]() Āś×ć
Āś×ć![]() £¬Ēó
£¬Ēó![]() µÄÖµ£»
掙术
£Ø2£©Čō![]() ”¢
Ӣ![]() Ӣ
”¢![]() ĪŖČżøö²»ĪŖ
ĪŖČżøö²»ĪŖ![]() µÄÓŠĄķŹż£¬ĒŅ
µÄÓŠĄķŹż£¬ĒŅ![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com