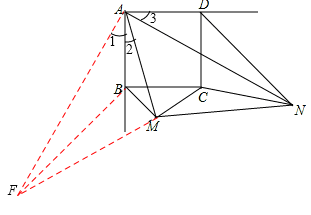
试题分析:(1)如图(3)由条件可以得出∠BMA=∠3,∠ABM=∠ADN=135°,就可以得出△ABM∽△NDA,利用相似三角形的性质就可以的得出BM•DN=a
2;(2)由△ABM∽△NDA,可以得出BM:DA=AB:ND,再由正方形的性质通过等量代换就可以得出△BCM∽△DNC,利用角的关系和圆周角的度数就可以求出结论;(3)将△AND绕点A顺时针旋转90°得到△ABF,连接MF,证明△ABF≌△ADN.利用边角的关系得出△BMF是直角三角形,由勾股定理就可以得出结论.
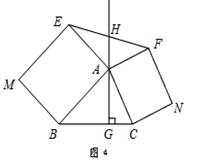
试题解析:(1)∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°.
∵BM,DN分别平分正方形的两个外角,∴∠CBM=∠CDN="45°." ∴∠ABM=∠ADN=135°.
∵∠MAN=45°,∴∠BMA=∠NAD. ∴△ABM∽△NDA. ∴
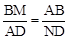
. ∴BM•DN=a
2.
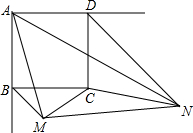
(2)由(1)△ABM∽△NDA可得BM:DA=AB:ND.
∵四边形ABCD是正方形,∴AB=DC,DA=BC,∠ABC=∠BCD=∠ADC=∠BAD=90°.
∴BM:BC=DC:ND.
∵BM,DN分别平分正方形ABCD的两个外角,∴∠CBM=∠NDC=45°.
∴△BCM∽△DNC.∴∠BCM=∠DNC.
∴∠MCN=360°-∠BCD-∠BCM-∠DCN=270°-(∠DNC+∠DCN)=270°-(180°-∠CDN)=135°.
(3)线段BM,DN和MN之间的等量关系是BM
2+DN
2=MN
2.证明如下:
如图,将△AND绕点A顺时针旋转90°得到△ABF,连接MF.则△ABF≌△ADN.
∴∠1=∠3,AF=AN,BF=DN,∠AFB=∠AND.∴∠MAF=∠1+∠2=∠2+∠3=∠BAD-∠MAN=45°.
∴∠MAF=∠MAN.
又∵AM=AM,∴△AMF≌△AMN.∴MF=MN.
可得∠MBF=(∠AFB+∠1)+45°=(∠AND+∠3)+45°=90°.
∴在Rt△BMF中,BM
2+BF
2=FM
2.
∴BM
2+DN
2=MN
2.

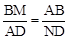 . ∴BM•DN=a2.
. ∴BM•DN=a2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

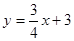 的图像分别交
的图像分别交 轴、
轴、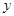 轴于
轴于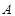 、
、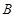 两点,且点
两点,且点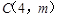 在一次函数
在一次函数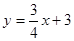 的图像上,
的图像上,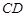 ⊥
⊥ 轴于点
轴于点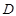 .
.
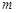 的值及
的值及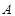 、
、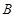 两点的坐标;
两点的坐标;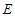 在线段
在线段 上,且
上,且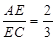 ,求
,求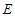 点的坐标;
点的坐标;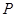 在
在 轴上,那么当△
轴上,那么当△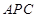 与△
与△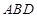 相似时,求点
相似时,求点 的坐标.
的坐标.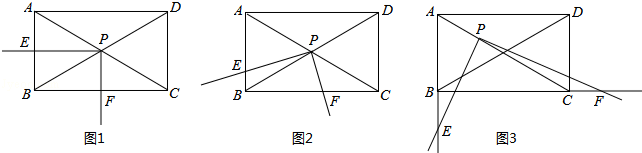
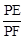 的值为 ;
的值为 ;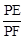 的值;
的值;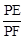 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.