
【题目】如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )

A.①③④B.①②④C.②③④D.①②③④
【答案】B
【解析】
①由非负数的性质,即可证得y2=﹣(x﹣2)2﹣1≤﹣1<0,即可得无论x取何值,y2总是负数;
②由抛物线l1:y1=a(x+1)2+2与l2:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),可求得a的值,然后由抛物线的平移的性质,即可得l2可由l1向右平移3个单位,再向下平移3个单位得到;
③由 y1﹣y2=﹣(x+1)2+2﹣[﹣(x﹣2)2﹣1]=﹣6x+6,可得随着x的增大,y1﹣y2的值减小;
④首先求得点A,C,D,E的坐标,即可证得AF=CF=DF=EF,又由AC⊥DE,即可证得四边形AECD为正方形.
解:①∵(x﹣2)2≥0,
∴﹣(x﹣2)2≤0,
∴y2=﹣(x﹣2)2﹣1≤﹣1<0,
∴无论x取何值,y2总是负数;
故①正确;
②∵抛物线G:y1=a(x+1)2+2与抛物线H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),
∴当x=1时,y=﹣2,
即﹣2=a(1+1)2+2,
解得:a=﹣1;
∴y1=﹣(x+1)2+2,
∴H可由G向右平移3个单位,再向下平移3个单位得到;
故②正确;
③∵y1﹣y2=﹣(x+1)2+2﹣[﹣(x﹣2)2﹣1]=﹣6x+6,
∴随着x的增大,y1﹣y2的值减小;
故③错误;
④设AC与DE交于点F,
∵当y=﹣2时,﹣(x+1)2+2=﹣2,
解得:x=﹣3或x=1,
∴点A(﹣3,﹣2),
当y=﹣2时,﹣(x﹣2)2﹣1=﹣2,
解得:x=3或x=1,
∴点C(3,﹣2),
∴AF=CF=3,AC=6,
当x=0时,y1=1,y2=﹣5,
∴DE=6,DF=EF=3,
∴四边形AECD为平行四边形,
∴AC=DE,
∴四边形AECD为矩形,
∵AC⊥DE,
∴四边形AECD为正方形.
故④正确.
故选:B.



科目:初中数学 来源: 题型:
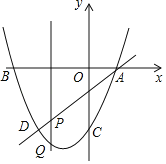
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
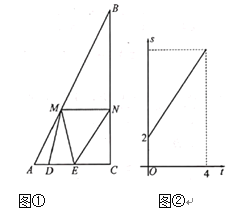
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() 点
点![]() 是
是![]() 上位于点
上位于点![]() 右侧的动点,点
右侧的动点,点![]() 是
是![]() 上的动点,在运动过程中始终保持
上的动点,在运动过程中始终保持![]() ,
,![]() cm.过
cm.过![]() 作
作![]() 交
交![]() 于
于![]() ,当点
,当点![]() 与点
与点![]() 重合时点
重合时点![]() 停止运动.设
停止运动.设![]() 的而积为
的而积为![]() ,点
,点![]() 的运动时问为
的运动时问为![]() ,
,![]() 与
与![]() 的函数关系如图②所示:
的函数关系如图②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
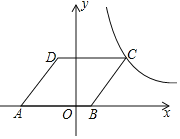
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的中点,一块足够大的三角板的直角顶点与点
的中点,一块足够大的三角板的直角顶点与点![]() 重合,将三角板绕点
重合,将三角板绕点![]() 旋转,三角板的两直角边分别交
旋转,三角板的两直角边分别交![]() 或它们的延长线)于点
或它们的延长线)于点![]() ,设
,设![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
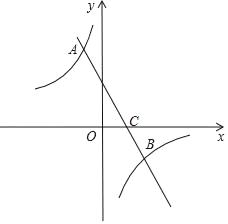
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(﹣
(m≠0)交于点A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直线与双曲线的解析式.
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
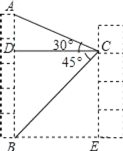
【题目】小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
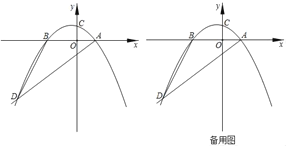
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)交x轴于点A(2,0),B(﹣3,0),交y轴于点C,且经过点d(﹣6,﹣6),连接AD,BD.
(1)求该抛物线的函数关系式;
(2)若点M为X轴上方的抛物线上一点,能否在点A左侧的x轴上找到另一点N,使得△AMN与△ABD相似?若相似,请求出此时点M、点N的坐标;若不存在,请说明理由;
(3)若点P是直线AD上方的抛物线上一动点(不与A,D重合),过点P作PQ∥y轴交直线AD于点Q,以PQ为直径作⊙E,则⊙E在直线AD上所截得的线段长度的最大值等于 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某市出台了民生兜底、医保脱贫、教育教助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为![]() 类贫困户。为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
类贫困户。为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
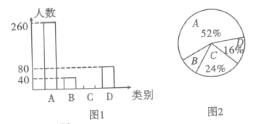
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户;
(2)抽查了多少户![]() 类贫困户?并补全统计图;
类贫困户?并补全统计图;
(3)若该地共有1300户贫困户,请估计至少得到4项帮扶措施的大约有多少户;
(4)为更好地做好精准扶贫工作,现准备从![]() 类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com