
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
【答案】(1)B(![]() ,1);(2)∠ABQ=90°,始终不变.(3)P的坐标为(﹣
,1);(2)∠ABQ=90°,始终不变.(3)P的坐标为(﹣![]() ,0)
,0)
【解析】
试题分析:(1)如图,作辅助线;证明∠BOC=30°,OB=2,借助直角三角形的边角关系即可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即可解决问题;
(3)根据点P在x的正半轴还是负半轴两种情况讨论,再根据全等三角形的性质即可得出结果.
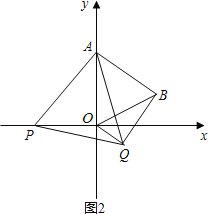
解:(1)如图1,过点B作BC⊥x轴于点C,
∵△AOB为等边三角形,且OA=2,
∴∠AOB=60°,OB=OA=2,
∴∠BOC=30°,而∠OCB=90°,
∴BC=![]() OB=1,OC=
OB=1,OC=![]() ,
,
∴点B的坐标为B(![]() ,1);
,1);
(2)∠ABQ=90°,始终不变.理由如下:
∵△APQ、△AOB均为等边三角形,
∴AP=AQ、AO=AB、∠PAQ=∠OAB,
∴∠PAO=∠QAB,
在△APO与△AQB中,
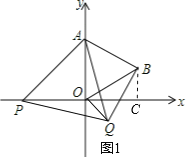
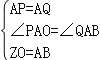 ,
,
∴△APO≌△AQB(SAS),
∴∠ABQ=∠AOP=90°;
(3)当点P在x轴负半轴上时,点Q在点B的下方,
∵AB∥OQ,∠BQO=90°,∠BOQ=∠ABO=60°.
又OB=OA=2,可求得BQ=![]() ,
,
由(2)可知,△APO≌△AQB,
∴OP=BQ=![]() ,
,
∴此时P的坐标为(﹣![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C′处;作∠BPC′的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.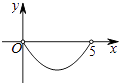
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的![]() .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片的一角斜折过去,点B落在点D处,EF为折痕,再把FC折过去与FD重合,FH为折痕,问:
(1)EF与FH有什么位置关系?
(2)∠CFH与∠BEF有什么数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
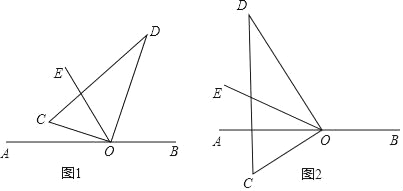
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>9且x<26,单位:km)

(1)说出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶了多少路程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com