
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:

①AP=EF;②∠PFE=∠BAP;③PD=![]() EC;④△APD一定是等腰三角形.
EC;④△APD一定是等腰三角形.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】由四边形ABCD是正方形可以得出AB=BC=CD=AD,∠1=∠2=45°,作PH⊥AB于H,可以得出四边形BEPH为正方形,可以得出AH=CE,由条件可以得出四边形PECF是矩形,就有CE=PF,利用三角形全等可以得出AP=EF,∠PFE=∠BAP,由勾股定理可以得出PD=![]() PF,可以得出PD=
PF,可以得出PD=![]() EC,点P在BD上要使△APD一定是等腰三角只有AP=AD、PA=PD或DA=DP时才成立,故可以得出答案.
EC,点P在BD上要使△APD一定是等腰三角只有AP=AD、PA=PD或DA=DP时才成立,故可以得出答案.
作PH⊥AB于H,
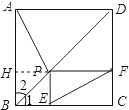
∴∠PHB=90°,
∵PE⊥BC,PF⊥CD,
∴∠PEB=∠PEC=∠PFC=90°.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠1=∠2=∠BDC=45°,∠ABC=∠C=90°,
∴四边形BEPH和四边形PECF是矩形,PE=BE,DF=PF,
∴四边形BEPH为正方形,
∴BH=BE=PE=HP,
∴AH=CE,
∴△AHP≌△FPE,
∴AP=EF,∠PFE=∠BAP,
故①、②正确,
在Rt△PDF中,由勾股定理,得
PD=![]() PF,
PF,
∴PD=![]() CE.
CE.
故③正确.
∵点P在BD上,
∴当AP=AD、PA=PD或DA=DP时△APD是等腰三角形.
∴△APD是等腰三角形只有三种情况.
故④错误,
∴正确的个数有3个.
故选C.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)20+(﹣14)﹣(﹣18)﹣13; (2)﹣2![]() ;
;
(3)(﹣7)×(﹣5)﹣90÷(﹣15) (4)-120×![]() +(-7)×
+(-7)×![]() +37×
+37×![]()
(5)﹣14﹣(1﹣0.5)×![]() ×[2-(-3)2].
×[2-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水池有三个流量相同的注排两用水管,开一个水管一个小时注排水![]() 立方米.假设先开一个进水管注满半池水,再同时开三个进水管注满另一半池水;排水时,先用
立方米.假设先开一个进水管注满半池水,再同时开三个进水管注满另一半池水;排水时,先用![]() 时间开三个水管同时排水,再用
时间开三个水管同时排水,再用![]() 时间只开一个水管排水,把池中水排尽,这样排完一池水所花时间比前面注满一池水少用
时间只开一个水管排水,把池中水排尽,这样排完一池水所花时间比前面注满一池水少用![]() 个小时,水池的容积是________立方米.
个小时,水池的容积是________立方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
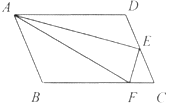
【题目】如图,在□ABCD中,点E是CD的中点,点F是BC边上的一点,且EF⊥AE.求证:AE平分∠DAF.
小林同学读题后有一个想法,延长FE,AD交于点M,要证AE平分∠DAF,只需证△AMF是等腰三角形即可.请你参考小林的想法,完成此题的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个直七棱柱,它的底面边长都是![]() ,侧棱长是
,侧棱长是![]() ,观察这个棱柱,请回答下列问题:
,观察这个棱柱,请回答下列问题:
![]()
![]() 这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出
这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出![]() 棱柱有多少个面?
棱柱有多少个面?
![]() 这个七棱柱一共有多少条棱?它们的长度分别是多少?
这个七棱柱一共有多少条棱?它们的长度分别是多少?
![]() 这个七棱柱一共有多少个顶点?
这个七棱柱一共有多少个顶点?
![]() 通过对棱柱的观察,你能说出
通过对棱柱的观察,你能说出![]() 棱柱的顶点数与
棱柱的顶点数与![]() 的关系及棱的条数与
的关系及棱的条数与![]() 的关系吗?
的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com