
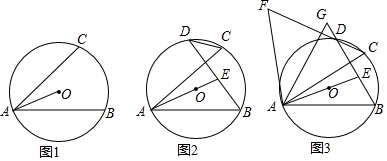
分析 (1)如图1中,连接OC、OB.只要证明△AOC≌△AOB即可.
(2)如图2中,连接EC.首先证明△EAC≌△EAB,推出EC=EB,∠ACE=∠B,再证明∠CDE=∠CED,推出CD=CE即可解决问题.
(3)连接AD,作AN⊥EC于N,AC与BD交于点M.设∠GAD=x.只要证明∠GAM=30°,在Rt△AGM中.AM=AN=AG•cos30°=$\frac{\sqrt{3}}{2}$AG,根据S△ACF=$\frac{1}{2}$•CF•AN=$\frac{\sqrt{3}}{4}$•CF•AG,即可解决问题.
解答 (1)证明:如图1中,连接OC、OB.
在△AOC和△AOB中,
$\left\{\begin{array}{l}{OA=OA}\\{OC=OB}\\{AC=AB}\end{array}\right.$,
∴△AOC≌△AOB,
∴∠CAO=∠BAO.
(2)证明:如图2中,连接EC.
在△AEC和△AEB中,
$\left\{\begin{array}{l}{AE=AE}\\{∠EAC=∠EAB}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△EAB,
∴EC=EB,∠ACE=∠B,
∵∠B=∠DCA,
∴∠DCA=∠ACE,
∵BD⊥AC,
∴∠CDE+∠DCA=90°,∠CED+∠ACE=90°,
∴∠CDE=∠CED,
∴CD=CE=EB.
(3)解:如图3中,连接AD,作AN⊥EC于N,AC与BD交于点M.设∠GAD=x.
∵∠B=50°,∠AMB=90°,
∴∠MAB=40°,
∴∠EAM=∠EAB=20°
∴∠CDM=∠CAB=40°,
∵CD=EC,AC⊥DE,
∴DM=ME,
∴AD=AE,
∴∠MAD=∠MAE=20°,
∴∠DAB=60°,
∴∠ADB=180°-∠DAB-∠B=70°,
∴∠ADN=180°-∠CDM=70°,
∴∠ADN=∠ADM,
∵AN⊥DF,AM⊥DB,
∴AN=AM,
∵∠GAB=45°+$\frac{1}{2}$∠GAE,
∴x+60°=45°+$\frac{1}{2}$(x+40°),
∴x=10°,
∴∠GAM=30°,
在Rt△AGM中.AM=AN=AG•cos30°=$\frac{\sqrt{3}}{2}$AG,
∴S△ACF=$\frac{1}{2}$•CF•AN=$\frac{\sqrt{3}}{4}$•CF•AG=$\frac{\sqrt{3}}{4}$×4=2$\sqrt{3}$.
点评 本题考查圆综合题、全等三角形的判定和性质、角平分线的性质定理、一元一次方程等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程,本题体现了数形结合的思想,本题的突破点是证明∠GAM=30°,属于中考压轴题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
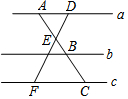 如图,直线a∥b∥c,若$\frac{AB}{BC}$=$\frac{4}{3}$,则$\frac{DE}{DF}$=$\frac{4}{7}$.
如图,直线a∥b∥c,若$\frac{AB}{BC}$=$\frac{4}{3}$,则$\frac{DE}{DF}$=$\frac{4}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.
如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com