
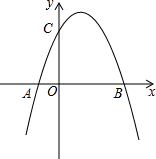
 如图,将抛物线y=-x2+1平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),并与x轴交于点C.
如图,将抛物线y=-x2+1平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),并与x轴交于点C.分析 (1)根据两根式以及抛物线平移a相同即可解决问题.
(2)求出顶点D坐标,只要证明∠ABD=∠ACB即可解决问题.
(3)如图2中,当点M在PA延长线时,作直线CE与PA交于点H,在PA取一点Q,使得EQ=EP,求出点Q坐标,根据FQ=AM,利用平移规律解决点M坐标.另外当点M在AP的延长线时,满足条件的点M不存在,
解答 解:(1)∵将抛物线y=-x2平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=-(x+1)(x-3)=-x2+2x+3,
即y=-x2+2x+3.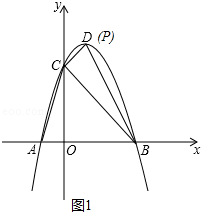
(2)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4).
∵y=-x2+2x+3,
∴当x=0时,y=3,即C点坐标为(0,3).
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°.
在△BCD中,∵BC2=32+32=18,CD2=12+12=2,BD2=22+42=20,
∴BC2+CD2=BD2.∴∠BCD=90°.
∴tan∠CBD=$\frac{CD}{BC}$=$\frac{\sqrt{2}}{\sqrt{18}}$=$\frac{1}{3}$
∵在△AOC中,∠AOC=90°,
∴tan∠ACO=$\frac{1}{3}$.
∴tan∠ACO=tan∠CBD.
∴∠ACO=∠CBD.
∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD.
∵点P是抛物线在第一象限上的一动点,∠ACB=∠ABP,
∴点P与点D重合,
∴所求点P坐标((1,4).
(3)如图2中,当点M在PA延长线时,作直线CE与PA交于点H,在PA取一点Q,使得EQ=EP,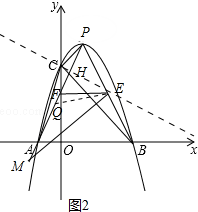
∵A(-1,0),P(1,4),
∴直线AP解析式为y=2x+2,
∵C(0,3),E(2,2),
∴直线CE的解析式为y=-$\frac{1}{2}$x+3,
∵2×(-$\frac{1}{2}$)=-1,
∴PA⊥EC,
由$\left\{\begin{array}{l}{y=2x+2}\\{y=-\frac{1}{2}x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=\frac{14}{5}}\end{array}\right.$,
∴HP=HQ,
∴点Q坐标(-$\frac{1}{5}$,$\frac{8}{5}$),
∵∠MEB=3∠MPE=∠MPE+∠PME,
∴∠MPE=2∠PME,
∵∠MPE=∠EQP=∠PME+∠QEM,
∴∠QEM=∠QME,
∴QM=QE,
∵PE=QE=AF=QM=$\sqrt{5}$,
∴FQ=AM,
∵点F向下平移$\frac{1}{5}$单位,向左平移$\frac{2}{5}$单位得到点Q,
∴点A向下平移$\frac{1}{5}$单位,向左平移$\frac{2}{5}$单位得到点M,
∴点M坐标为(-$\frac{6}{5}$,-$\frac{2}{5}$).
当点M在AP的延长线时,满足条件的点M不存在,
综上所述,满足条件的点M坐标为(-$\frac{6}{5}$,-$\frac{2}{5}$).
点评 本题考查二次函数综合题、二次函数的应用、锐角三角函数、勾股定理、平移的鞥知识,解题的关键是熟练应用这些知识解决问题,学会利用特殊点解决问题,学会3倍角的转化,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 已知:如图,在正方形ABCD中,E,F分别AB,AD上的点,又AB=12,EF=10,△AEF的面积等于五边形EBCDF面积的$\frac{1}{5}$,求AE,AF的长.
已知:如图,在正方形ABCD中,E,F分别AB,AD上的点,又AB=12,EF=10,△AEF的面积等于五边形EBCDF面积的$\frac{1}{5}$,求AE,AF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△AOB与△COD是位似图形,它们的对应线段之比是1:3.
如图,△AOB与△COD是位似图形,它们的对应线段之比是1:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线AB与CD相交于O,OE、OF分别是∠BOD、AOD平分线,
如图,已知直线AB与CD相交于O,OE、OF分别是∠BOD、AOD平分线,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com