
 ,求点E的坐标;
,求点E的坐标; 的值.
的值.
 ,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值.
,仿照(1)的方法,可通过△OEF∽△BAO,求得EF的长,而△AEF∽△APO,根据相似三角形所得比例线段即可求得OP的长即t的值. ;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有:
;由(2)证得△AOE∽△PBD,那么AE:PD=OA:PB,由于OA=3,PB=OB-OP=1,因此AE=3PD,可设PD=x,则AE=3x,易得△AEC∽△ADP,则有: ,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值.
,根据射影定理可在Rt△ABO中求出AC的长,利用勾股定理可求得EC的表达式,将它们代入上式比例式中,即可求得x的值,进而可得到EC、AE的长,有了AE、AP的长,即可得到AE:EP的值. ,OA=3,
,OA=3, ,即
,即 ,所以OF=
,所以OF= ,
, ).
). ∠AEO=∠PDB=90°+∠PAB,
∠AEO=∠PDB=90°+∠PAB, ;
; ,即
,即 ,所以EF=
,所以EF= ,
, ,即
,即 ,所以t=
,所以t= ,
, ;
; .
.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源:2010年河北省邯郸市中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年中考数学全真模拟试卷(解析版) 题型:选择题

 +1=c
+1=c查看答案和解析>>
科目:初中数学 来源:2010年河北省邯郸市中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年河北省邯郸市中考数学一模试卷(解析版) 题型:选择题
 (其中k是使
(其中k是使 为奇数的正整数),并且运算重复进行.例如:取n=26,则:
为奇数的正整数),并且运算重复进行.例如:取n=26,则: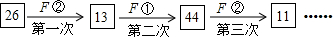 若n=15,则第15次“F”运算的结果是( )
若n=15,则第15次“F”运算的结果是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com