
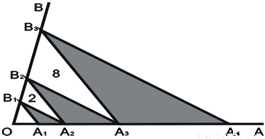
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3,若△A2B1B2、△A3B2B3的面积分别为2和8,则阴影部分的面积和= 。
21
【解析】
试题分析:已知△A2B1B2,△A3B2B3的面积分别为2,8,且两三角形相似,因此可得出A2B2:A3B3=1:2,由于△A2B2A3与△B2A3B3是等高不等底的三角形,所以面积之比即为底边之比,因此这两个三角形的面积比为1:2,根据△A3B2B3的面积为8,可求出△A2B2A3的面积,同理可求出△A3B3A4和△A1B1A2的面积.即可求出阴影部分的面积.
∵A2B2∥A3B3,A2B1∥A3B2,
∴∠OB2A2=∠OB3A3,∠A2B1B2=∠A3B2B3,
∴△B1B2A2∽△B2B3A3,
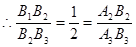
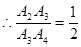

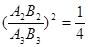 ,,△A3B2B3的面积是8,
,,△A3B2B3的面积是8,
∴△A2B2A3的面积为=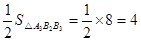
同理可得:△A3B3A4的面积=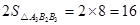
△A1B1A2的面积=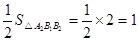
∴三个阴影面积之和=1+4+16=21.
考点:本题考查的是平行线的性质,相似三角形的判定和性质
点评:解答本题的关键是利用平行线证明三角形相似,再根据已给的面积,求出相似比,从而求阴影部分的面积.


科目:初中数学 来源: 题型:
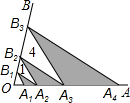 如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为查看答案和解析>>
科目:初中数学 来源: 题型:
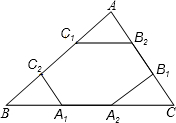 如图,点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,若△ABC的周长为L,则六边形A1A2B1B2C1C2的周长为( )
如图,点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,若△ABC的周长为L,则六边形A1A2B1B2C1C2的周长为( )A、
| ||
| B、3L | ||
| C、2L | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
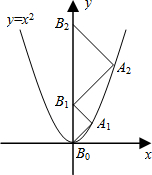 如图,点A1、A2、A3、…、An在抛物线y=x2图象点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2012B2011B2012的腰长=
如图,点A1、A2、A3、…、An在抛物线y=x2图象点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2012B2011B2012的腰长=| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2013B2012B2013的腰长=
如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形(点B0是坐标原点),则△A2013B2012B2013的腰长=| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
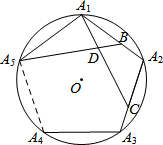 (2013•南京二模)如图,点A1、A2、A3、A4、A5在⊙O上,且
(2013•南京二模)如图,点A1、A2、A3、A4、A5在⊙O上,且 |
| A1A2 |
 |
| A2A3 |
 |
| A3A4 |
 |
| A4A5 |
 |
| A5A1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com