解:(1)原式=

+(-2)-2×

+1=

-1;
(2)原方程可变形为:x
2-2(m+1)x+m
2=0,
∵x
1、x
2是方程的两个根,
∴△≥0,即4(m+1)
2-4m
2≥0,
∴8m+4≥0,
解得:m≥-

,
又x
1、x
2满足|x
1|=x
2,
∴x
1=x
2或x
1=-x
2,即△=0或x
1+x
2=0,
由△=0,即8m+4=0,得m=-

,
由x
1+x
2=0,即:2(m+1)=0,得m=-1,(不合题意,舍去),
则当|x
1|=x
2时,m的值为-

.
分析:(1)原式第二项利用负指数幂法则计算,第三项利用特殊角的三角函数值化简,最后一项利用零指数幂法则计算,即可得到结果;
(2)将方程整理为一般形式,根据方程有解得到根的判别式的值大于等于0,列出关于m的不等式,求出不等式的解集得到m的范围,根据两根满足的关系式,利用绝对值的代数意义化简,即可求出满足题意m的值.
点评:此题考查了根的判别式,以及实数的运算,弄清题意是解本题的关键.

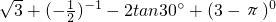 .
. +(-2)-2×
+(-2)-2× +1=
+1= -1;
-1; ,
, ,
, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案