
 如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为( )
如图,AD,AE分别是△ABC的角平分线和中线,CG⊥AD于F,交AB于G,若AB=8,AC=6,则EF的长为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:选择题
 一块三角形玻璃样板不慎被小强同学碰破,成了如图所示的四块,聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为可行的方案是( )
一块三角形玻璃样板不慎被小强同学碰破,成了如图所示的四块,聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板,你认为可行的方案是( )| A. | 带其中的任意两块去都可以 | B. | 带①、②或②、③去就可以了 | ||
| C. | 带①、④或③、④去就可以了 | D. | 带①、④或①、③去就可以了 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
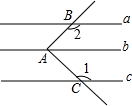 如图,直线a∥b∥c,直角∠BAC的顶点A在直线b上,两边分别于直线a、c相交于点B、C,则∠1+∠2的度数是( )
如图,直线a∥b∥c,直角∠BAC的顶点A在直线b上,两边分别于直线a、c相交于点B、C,则∠1+∠2的度数是( )| A. | 180° | B. | 210° | C. | 270° | D. | 360° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com