(2013•惠山区一模)一公司面向社会招聘人员,要求如下:①对象:机械制造类和规划设计类人员共150名;②机械类人员工资为600元/月,规划设计类人员为1000元/月.
(1)本次招聘规划设计人员不少于机械制造人员的2倍,若要使公司每月所付工资总额最少,则这两类人员各招多少名?此时最少工资总额是多少?
(2)在保证工资总额最少条件下,因这两类人员表现出色,公司领导决定另用20万元奖励他们,其中机械人员人均奖金不得超过规划人员的人均奖金,但不低于200元,试问规划设计类人员的人均奖金的取值范围.
【答案】
分析:(1)设机械制造人员招x名,所付工资总额为w元,则规划设计人员为2x,由“规划设计人员不少于机械制造人员的2倍”可得x的取值范围,由题意可得w关于x的表达式.
(2)设机械类人均奖金为a元,规划设计类人均奖金为b元.由题意得:
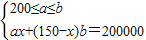
,求解可得.
解答:解:(1)设机械制造人员招x名,所付工资总额为w元,则由题意得:
w=600x+1000(150-x)(1分)=-400x+150000
∵150-x≥2x∴x≤50
∴当x=50时,w有最小值为-400×50+150000=130000元
∴本次招聘机械制造人员50名,规划设计人员100名,最少工资总额是130000元.
(2)设机械类人均奖金为a元,规划设计类人均奖金为b元.
由“其中机械人员人均奖金不得超过规划人员的人均奖金,但不低于200元”和“总额为20万”得:
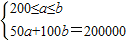
,
解得
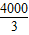
≤b≤1900.
所以规划设计类人员人均奖金范围为
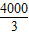
元至1900元之间.
点评:本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意利用一次函数求最值时,关键是应用一次函数的性质.

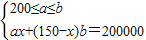 ,求解可得.
,求解可得.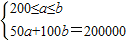 ,
,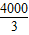 ≤b≤1900.
≤b≤1900.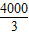 元至1900元之间.
元至1900元之间.
