
【题目】已知二次函数y= x2-4x+3.
(1)把这个二次函数化成![]() 的形式并写出抛物线的顶点坐标;
的形式并写出抛物线的顶点坐标;
(2)画出这个二次函数的图象,并利用图象直接写出当y>0时,x的取值范围. 当x取何值时,y随x的增大而减小;
(3)若抛物线与![]() 轴的交点记为A,B,该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
【答案】(1)![]() -1,(2,-1);(2)
-1,(2,-1);(2)![]() ,
,![]() ;
; ![]() ;(3)(4,3),(0,3)
;(3)(4,3),(0,3)
【解析】
(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式,根据顶点式即可求得顶点坐标.
(2)根据顶点坐标,抛物线与y轴的交点坐标以及抛物线与x轴的交点坐标画出图象,根据图象求得当y>0时,x的取值范围,当x<2,y随x的增大而减小;
(3)S△ABC=![]() ×AB×yC即可求解.
×AB×yC即可求解.
(1)y=x24x+3=(x2)21,则该抛物线解析式是y=(x2)21;
∴抛物线的顶点为(2,1);
(2)画出函数图象如图:
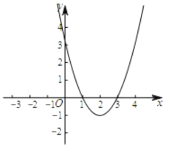
当y>0时,x的取值范围是x<1或x>3.当x<2,y随x的增大而减小;
(3)由图可知:A(1,0),B(3,0)
∴AB=2
∵S△ABC=![]() ×AB×yC=
×AB×yC=![]() ×2×3=3.
×2×3=3.
∴yC=3,故x24x+3=3,
解得x1=0,x2=4,
故C点(4,3),(0,3).


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边CD上(不与点C,D重合),连接AE,BD交于点F.
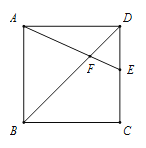
(1)若点E为CD中点,AB=2![]() ,求AF的长.
,求AF的长.
(2)若![]() ∠AFB=2,求
∠AFB=2,求![]() 的值.
的值.
(3)若点G在线段BF上,且GF=2BG,连接AG,CG,设![]() =x,四边形AGCE的面积为
=x,四边形AGCE的面积为![]() ,
,![]() ABG的面积为
ABG的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
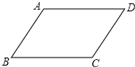
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“康河泛舟,问道剑桥”,甲乙两人相约泛舟康河,路线均为从![]() 到
到![]() 再返回
再返回![]() ,且
,且![]() 全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的
全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的![]() 地,甲到达目的地拍照5分钟便原速返回
地,甲到达目的地拍照5分钟便原速返回![]() 地;乙到达
地;乙到达![]() 地后休息了2分钟,然后立即提速为原速的
地后休息了2分钟,然后立即提速为原速的![]() 倍返回
倍返回![]() 地.甲乙之间的距离
地.甲乙之间的距离![]() (单位:米)与甲的行驶时间
(单位:米)与甲的行驶时间![]() (单位:分钟)之间的函数关系如图所示.则当乙回到
(单位:分钟)之间的函数关系如图所示.则当乙回到![]() 地时,甲距离
地时,甲距离![]() 地________米.
地________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有一个公共点,结合函数图象,求
.若抛物线与线段PQ恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
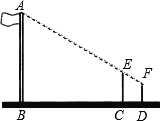
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解九年级A、B两个班级学生的跳绳成绩情况,在每个班各随机抽取20名同学(不分性别)测试每分钟跳绳次数,收集数据后制作成如下的统计图.

(1)已知一分钟跳绳次数在175次及以上的为成绩优秀,两个班的人数均为50人,请你估计一下,哪个班级优秀人数多?多几人?
(2)请你选择适当的统计量来说明哪个班级的整体成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
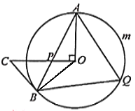
【题目】如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,点Q是弧AmB上的一点.
①求∠AQB的度数;
②若OA=18,求弧AmB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com