
【题目】如图,△ABC中,D是BC上的一点,AB=10,BD=6,AD=8,AC=17.
(1)判断AD与BC的位置关系,并说明理由;
(2)求△ABC的面积.

【答案】(1)AD⊥BC.理由见解析; (2) 84.
【解析】
(1)根据AB=10,BD=6,AD=8,可得BD2+AD2=AB2,根据勾股定理的逆定理可进行判定△ABD是直角三角形,即∠ADB=90°,
(2) 在Rt△ACD中,根据CD2=AC2-AD2=172-82=152,可得CD=15,进而可得S△ABC=![]() BC·AD=
BC·AD=![]() (BD+CD)·AD=
(BD+CD)·AD=![]() ×21×8=84
×21×8=84
(1)AD⊥BC.理由如下:
因为BD2+AD2=62+82=102=AB2,
所以△ABD是直角三角形,且∠ADB=90°,
所以AD⊥BC.
(2)在Rt△ACD中,因为CD2=AC2-AD2=172-82=152,所以CD=15,
所以S△ABC=![]() BC·AD=
BC·AD=![]() (BD+CD)·AD=
(BD+CD)·AD=![]() ×21×8=84.
×21×8=84.


科目:初中数学 来源: 题型:
【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F.试猜想EF、BE、CF之间有怎样的关系,并说明理由.


(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,则刚才的结论还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为 . 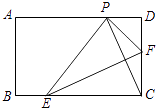
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题: 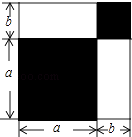
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节,小丽独自一人去老家玩,家住在车站附近的姑姑到车站去接小丽.因为担心小丽下车后找不到路,姑姑一路小跑来到车站,结果客车晚点,休息一阵后,姑姑接到小丽,和小丽一起慢慢的走回了家.下列图象中,能反映以上过程中小丽姑姑离家的距离s与时间t的关系的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场经营的某品牌童装,4月的销售额为20000元,为扩大销量,5月份商场对这种童装打9折销售,结果销量增加了50件,销售额增加了7000元.
(1)求该童装4月份的销售单价;
(2)若4月份销售这种童装获利8000元,6月全月商场进行“六一儿童节”促销活动.童装在4月售价的基础上一律打8折销售,若该童装的成本不变,则销量至少为多少件,才能保证6月的利润比4月的利润至少增长25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
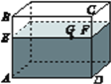
【题目】有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上. 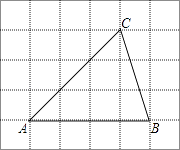
(1)△ABC的面积等于;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人从A城出发,前往距离A城30千米的B城.现在有三种方案供他选择:
①骑自行车,其速度为15千米/时;
②蹬三轮车,其速度为10千米/时;
③骑摩托车,其速度为40千米/时.
(1)选择哪种方式能使他从A城到达B城的时间不超过2小时?请说明理由;
(2)设此人在行进途中离B城的距离为s(千米),行进时间为t(时),就(1)所选定的方案,试写出s与t之间的函数关系式(注明自变量t的取值范围),并在如图所示的平面直角坐标系中画出函数的图象.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com