
����Ŀ����֪����ͼ1����A��O��B������ֱ��MN�ϣ��ֽ�����OA�Ƶ�O��˳ʱ�뷽����ÿ��2����ٶ���ת��ͬʱ����OB�Ƶ�O����ʱ�뷽����ÿ��4����ٶ���ת����ͼ2������תʱ��Ϊt��0���t��90�룩��
��1���ú�t�Ĵ���ʽ��ʾ��MOA�Ķ�����
��2�����˶������У�����AOB�ڶ��δﵽ60��ʱ����t��ֵ��
��3������ת�������Ƿ����������t��ʹ������OB��������OM������OA������ON�е�����������ɵĽǣ�ָ����0���������180��Ľǣ���ƽ���ߣ�������ڣ���ֱ��д��t��ֵ����������ڣ���˵�����ɣ�

���𰸡���1����MOA=2t����2��t=40��ʱ����AOB�ڶ��δﵽ60�㣻��3����t��ֵ�ֱ�Ϊ18��22.5��36��60��67.5��ʱ������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���ߣ�
��������
�����������1����AOM�Ķ�������OA��ת�ٶȳ�����תʱ�䣻
��2������AOB�ڶ��δﵽ60��ʱ������OB��OA����࣬������AOM+��BON����MON=60���з������ɵã�
��3������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���������������
��OB����ƽ����AOMʱ������![]() ��AOM=��BOM���з�����⣬
��AOM=��BOM���з�����⣬
��OB����ƽ����MONʱ��������BOM=![]() ��MON���з�����⣬
��MON���з�����⣬
��OBƽ����AONʱ��������BON=![]() ��AON���з�����⣮
��AON���з�����⣮
�⣺��1����MOA=2t��
��2����ͼ��
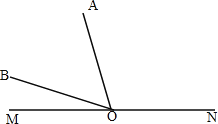
��������֪����AOM=2t����BON=4t��
����AOB�ڶ��δﵽ60��ʱ����AOM+��BON����MON=60����
��2t+4t��180=60����ã�t=40��
��t=40��ʱ����AOB�ڶ��δﵽ60�㣻
��3������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ�������������������
��OBƽ����AOMʱ����![]() ��AOM=��BOM��
��AOM=��BOM��
��t=180��4t����t=4t��180��
��ã�t=36��t=60��
��OBƽ����MONʱ���ߡ�BOM=![]() ��MON������BOM=90����
��MON������BOM=90����
��4t=90����4t��180=90��
��ã�t=22.5����t=67.5��
��OBƽ����AONʱ���ߡ�BON=![]() ��AON��
��AON��
��4t=![]() ��180��2t������180����4t��180��=
��180��2t������180����4t��180��=![]() ��180��2t����
��180��2t����
��ã�t=18��t=90�����������⣬��ȥ����
���ϣ���t��ֵ�ֱ�Ϊ18��22.5��36��60��67.5��ʱ������OB��������OM������OA������ON�е�����������ɵĽǵ�ƽ���ߣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ���½�һ������ΪL�Ķ��鳤�ȣ����������ɿ���л��ƺ�û�л��Ƶ����ֹ���С��ͬ�������ε���ש������һ�𣬰�ͼ����ʾ�Ĺ���ƴ��ͼ���������ȣ���֪ÿ��С�����ε���ש�ı߳���Ϊ0.3m��

��1����ͼʾ���ɣ���һͼ���ij���L1= ���ڶ���ͼ���ij���L2= ��
��2�����ô���ʽ��ʾ���л��Ƶĵ���ש����n�����ȵij���Ln��m��֮��Ĺ�ϵ��
��2�������ȵij���LΪ30.3mʱ��������������л���ͼ���Ĵ�ש�Ŀ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ݵ��ݱں�ȴ�Լ��0.0007mm��0.0007�ÿ�ѧ��������ʾΪ�� ��
A��0.7��10��3 B��7��10��3 C��7��10��4 D��7��10��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��2����3������x��ĶԳƵ���__________������y��ĶԳƵ���__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ���������ݣ��ٽ�����⣬
���⣺��m2+2mn+2n2��6n+9=0����m��n��ֵ��
�⣺��m2+2mn+2n2��6n+9=0
��m2+2mn+n2+n2��6n+9=0
����m+n��2+��n��3��2=0
��m+n=0��n��3=0
��m=��3��n=3
���⣨1����x2+2y2��2xy+4y+4=0����xy��ֵ��
��2����֪a��b��c����ABC�����߳�������a2+b2=10a+8b��41����c����ABC����ıߣ���c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij������ҵ�ֵ���ڣ���ѧ������ȤС���ͬѧ����������ѧ��֪ʶ��������֧�ܵ���ߵ�E������ľ���EF����������֧�ܵ�����BC����洹ֱ������BCA=90������BC=1.5m����F��A��C��ͬһ��ˮƽ���ϣ�б��AB��ˮƽ��AC�ļн���BAC=30����֧�Ÿ�DE��AB�ڵ�D����֧�ܵı�BE��AB�ļн���EBD=60�����ֲ��AD=1m�����������֧�ܵı�BE������E������ľ���EF�ij��ȣ�
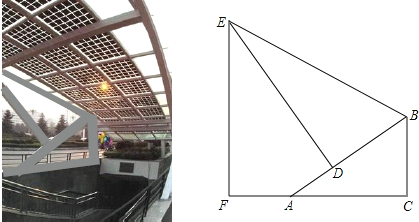
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲˻���������ܲ�����8390ǧ�ˣ��ڶ���ȵ�һ����560ǧ�ˣ�������ȵ�һ���![]() ��1200ǧ�����������������ǧ���߲�?
��1200ǧ�����������������ǧ���߲�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У�AD��BC��D����AB=4cm��AD=2![]() cm��EΪAB���е㣬PΪAD��һ�㣬PE+PB����СֵΪ ��
cm��EΪAB���е㣬PΪAD��һ�㣬PE+PB����СֵΪ ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com