
����Ŀ��С���İְֿ�������С���ڹ�·��������ʻ��С��ÿ��һ��ʱ�俴������̱��ϵ������£�
ʱ�� | 12��00 | 13��00 | 14��30 |
���ϵ��� | ��һ����λ��������֮����6 | ��һ����λ����ʮλ���λ������12��00ʱ�����������õߵ��� | ��12��00ʱ��������λ���м���˸�0 |
��12��00ʱ��������λ���Ƕ��٣���12��00ʱ��������λ���ĸ�λ��Ϊy��ʮλ��Ϊx���г��Ķ�Ԫһ�η�����Ϊ_____��
 �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ.
��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ.
��1��������![]() ����
����![]() ��ԳƵ���
��ԳƵ���![]() ����д����
����д����![]() ����������ꣻ
����������ꣻ
��2������![]() ����ƽ��6����λ������ƽ�ƺ����
����ƽ��6����λ������ƽ�ƺ����![]() ����д����
����д����![]() ����������ꣻ
����������ꣻ
��3���۲���![]() ����
����![]() �������Ƿ����ijֱ�߶Գƣ����ǣ����ô����������Գ��ᣮ
�������Ƿ����ijֱ�߶Գƣ����ǣ����ô����������Գ��ᣮ
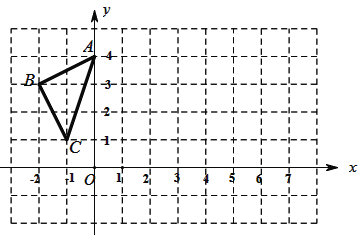
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
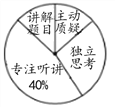
����Ŀ��ij������������Ϊ�˽������ѧ������ѧ������������������������ɡ�����˼����רע������������Ŀ���ĸ���Ŀ�������ۣ����С�������鲿��ѧУ������ѧ�����������ѧ���Ŀ��ò���������Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ�������������������ͳ��ͼ�е���Ϣ����������⣺
��1����������������� ��
��2��������ͳ��ͼ�У����������ɡ���Ӧ��Բ�Ľ�Ϊ �ȣ�
��3��������ͳ��ͼ����������
��4������õ�������ѧ������60000������ô�ڿ�������������˼������ѧ��Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����OA=OC�������н��ۣ�
��abc��0����![]() ��0����ac��b+1=0����OAOB=��
��0����ac��b+1=0����OAOB=��![]() ��
��
������ȷ���۵ĸ����ǣ� ��

A��4 B��3 C��2 D��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��![]() +bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����
��1���������ߵĽ���ʽ����Գ��᷽�̣�
��2������AC��BC�����ж���AOC����COB�Ƿ����ƣ���˵�����ɣ�
��3������������BC֮���Ƿ����һ��D��ʹ����DBC���������������������D���������DBC��������������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�������������У�����A������Ϊ��0��3������Ҫ��ش��������⣺

��1����ͼ�н�����ȷ��ƽ��ֱ������ϵ��
��2��ֱ��д����ABC�������
��3������һ����ACD��ʹ��AD��![]() ��CD��
��CD��![]() ����д����D�����꣮
����д����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�AD//BC���Խ���AC��BD���ڵ�O����AC=BD�������ĸ��������������ǣ� ��
A. ��AB=CD�����ı���ABCDһ���ǵ������Σ�
B. ����DBC=��ACB�����ı���ABCDһ���ǵ������Σ�
C. ��![]() �����ı���ABCDһ���Ǿ��Σ�
�����ı���ABCDһ���Ǿ��Σ�
D. ��AC��BD��AO=OD�����ı���ABCDһ���������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=kx+b��x���ڵ�A����y���ڵ�B��ֱ��y=2x��4��x���ڵ�D����ֱ��AB�ཻ�ڵ�C��3��2����
��1������ͼ��д������x�IJ���ʽ2x��4��kx+b�Ľ⼯��
��2������A������Ϊ��5��0������ֱ��AB�Ľ���ʽ��
��3���ڣ�2���������£����ı���BODC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȷֽǡ�����ѧʷ��һ�����������⣬�����ó߹治���ܡ����ȷֽǡ�����������ѧ������˹��������������һ�֡����ȷ���ǡ��ķ�������ͼ��������������ǡ�AOB����ֱ������ϵ�У���OB��x���ϡ���OA�뺯��![]() ��ͼ���ڵ�P����PΪԲ�ġ���2OPΪ�뾶������ͼ���ڵ�R���ֱ����P��R��x���y���ƽ���ߣ���ֱ���ཻ�ڵ�M������OM�õ���MOB�����MOB=
��ͼ���ڵ�P����PΪԲ�ġ���2OPΪ�뾶������ͼ���ڵ�R���ֱ����P��R��x���y���ƽ���ߣ���ֱ���ཻ�ڵ�M������OM�õ���MOB�����MOB=![]() ��AOB��Ҫ��������˹�ķ��������о��������⣺
��AOB��Ҫ��������˹�ķ��������о��������⣺
��1����P��![]() ��
��![]() ����R��
����R��![]() ��
��![]() ������ֱ��OM��Ӧ�ĺ�������ʽ���ú�
������ֱ��OM��Ӧ�ĺ�������ʽ���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���ֱ����P��R��y���x���ƽ���ߣ���ֱ���ཻ�ڵ�Q����˵��Q����ֱ��OM�ϣ����ݴ�֤����MOB=![]() ��AOB��
��AOB��
��3��Ӧ�����������õ��Ľ��ۣ���������ȷ�һ���۽ǣ������ּ�Ҫ˵����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com