
【题目】如图1:抛物线y=ax2+bx+3交x轴于点A、B,连接AC、BC,tan∠ABC=1,tan∠BAC=3.
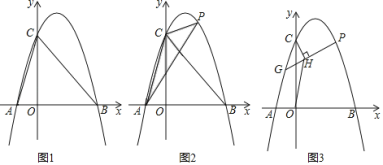
(1)求抛物线的解析式;
(2)如图2,点P在第一象限的抛物线上,连接PC、PA,若点P横坐标为t,△PAC的面积为S,求S与t的函数关系式;
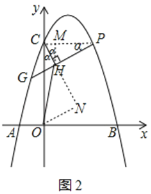
(3)在(2)的条件下,当S=3时,点G为第二象限抛物线上一点,连接PG,CH⊥PG于点H,连接OH,若tan∠OHG=![]() ,求GH的长.
,求GH的长.
【答案】(1)y=﹣x2+2x+3;(2)S=![]() t2+
t2+![]() t;(3)GH=
t;(3)GH=![]()
【解析】
(1)根据解析式得到OC=3,再根据已知条件求出点A、B的坐标即可求出解析式;
(2)根据点A、P的坐标求出直线AP的解析式,得到直线与y轴交点R的坐标,即可求出S与t的函数关系式;
(3)先求出点P的坐标得到CP∥x轴,作CH⊥GP,作HM⊥CP,过点O作ON⊥CH交CH的延长线于点N,分别求出CH、ON、CN,根据tan∠OHG=![]() 求出点H的坐标,根据直线PG求出点G的坐标,即可得到答案.
求出点H的坐标,根据直线PG求出点G的坐标,即可得到答案.
解:(1)由题意得c=3,∴OC=3,
∵tan∠ABC=1,∴OB=3,
∵tan∠BAC=3,∴OA=1,
∴点A、B、C的坐标分别为:(﹣1,0)、(3,0)、(0,3),
则抛物线的表达式为:y=a(x+1)(x﹣3),
将点C坐标代入上式并解得:a=﹣1,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)点P(t,﹣t2+2t+3),点A(﹣1,0),

将点P、A坐标代入一次函数表达式y=kx+b并解得:
直线PA的表达式为:y=(3﹣t)(x+1),
设直线AP交y轴于点R,则R(0,3﹣t),
S=![]() CR×(xP﹣xA)=
CR×(xP﹣xA)=![]() (3﹣3+t)(t+1)=
(3﹣3+t)(t+1)=![]() t2+
t2+![]() t;
t;
(3)S=![]() t2+
t2+![]() t=3,解得:t=﹣3(舍去)或2,
t=3,解得:t=﹣3(舍去)或2,
∴点P(2,3),
∵点C(0,3),
连接CP,则CP∥x轴,
作CH⊥GP,则∠CPH=∠OCH=α,
作HM⊥CP,则∠CHM=∠HCO=α,
过点O作ON⊥CH交CH的延长线于点N,
CP=2,OC=3,
CH=CPsinα=2sinα,ON=OCsinα=3sinα,CN=OCcosα=3cosα,
∵ON⊥CN,GH⊥CH,
∴∠HON=∠OHG,
∴tan∠HON=![]() =tan∠OHG=
=tan∠OHG=![]() ,
,
解得:tan![]() ,则sinα=
,则sinα=![]() ,cosα=
,cosα=![]() ,
,
MH=CHcosα=2sinαcosα=![]() ,CM=CHsinα=
,CM=CHsinα=![]() ,
,
∴点H(![]() ,
,![]() );
);
设点G(m,﹣m2+2m+3),而点P(2,3),
由点G、P的坐标得,直线PG表达式中的k值为:﹣m=﹣tanα=-![]() ,
,
∴点G(﹣![]() ,
,![]() ),
),
由点G、H的坐标得,GH=![]() .
.


科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.
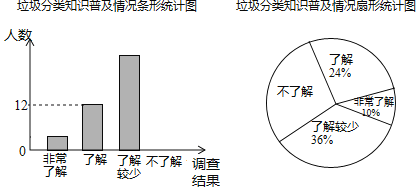
(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
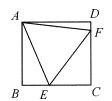
【题目】如图,在矩形 ABCD 中,点 E,F 分别在 BC,CD 边上,且 CE=3,CF=4.若△AEF 是等边三角形,则 AB 的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)及过格点的直线l.
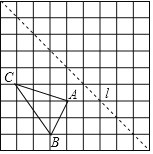
(1)画出△ABC关于直线l对称的△A1B1C1;
(2)将△ABC向上平移3个单位长度,再向左平移1个单位长度,画出平移后的△A2B2C2;
(3)以A、A1、A2为顶点的三角形中,tan∠A2AA1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.
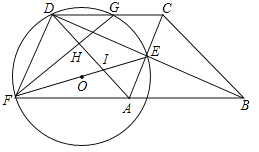
(1)求∠FDE的度数;
(2)试判断四边形FACD的形状,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:FD=FI;
②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
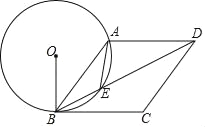
【题目】如图,点E在菱形ABCD的对角线BD上,连接AE,且AE=BE,⊙O是△ABE的外接圆,连接OB.
(1)求证:OB⊥BC;
(2)若BD=![]() ,tan∠OBD=2,求⊙O的半径.
,tan∠OBD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E,F,G分别是等边三角形ABC三边AB,BC,CA上的动点,且始终保持AE=BF=CG,设△EFG的面积为y,AE的长为x,y关于x的函数图象大致为图2所示,则等边三角形ABC的边长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com