

分析 (1)①由已知条件得出DE=BC=AB=8,BD=AB-AD=6,∠BDE=90°,由勾股定理求出BE即可;
②连接DG,由△ABC是等腰直角三角形得出△ADF是等腰直角三角形,得出∠AFD=∠A=45°,得出∠GFE=135°,由SAS证明△ABG≌△DEG,得出BG=EG,∠1=∠2,由AAS证明△BDG≌△EFG,得出对应角相等∠BGD=∠EGF,得出∠BGE=∠DGF=90°,即可得出结论;
(2)连接GF、DG,先证明△ADG是等边三角形,得出DG=AD,再证明四边形ADFG是菱形,得出GF=DF=AD=DG,∠EFG=∠ADF=120°,由SAS证明△BDG≌△EFG,得出BG=EG,∠BGD=∠EGF,证出∠BGE=∠DGF=60°,即可得出结论.
解答 解:(1)①∵AB=BC,DE=BC,
∴DE=BC=AB=8,
∵AD=2,
∴BD=AB-AD=6,
∵DE∥BC,
∴∠ADF=∠ABC=90°,
∴∠BDE=90°,
∴BE=$\sqrt{B{D}^{2}+D{E}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10;
②△BGE是等腰直角三角形;理由如下:
连接DG,如图1所示: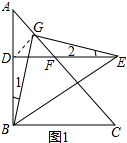
∵AB=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴△ADF是等腰直角三角形,
∴∠AFD=∠A=45°,
∴∠GFE=135°,
∵G是AF的中点,
∴DG=$\frac{1}{2}$AF=AG=FG,∠GDF=45°,∠DGF=90°,
∴∠A=∠GDF,
在△ABG和△DEG中,
$\left\{\begin{array}{l}{AB=DE}&{\;}\\{∠A=∠GDF}&{\;}\\{AG=DG}&{\;}\end{array}\right.$,
∴△ABG≌△DEG(SAS),
∴BG=EG,∠1=∠2,
∵∠BDG=90°+45°=135°,
∴∠BDG=∠GFE,
在△BDG和△EFG中,
$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{∠BDG=∠GFE}&{\;}\\{BG=EG}&{\;}\end{array}\right.$,
∴△BDG≌△EFG(AAS),
∴∠BGD=∠EGF,
∴∠BGE=∠DGF=90°,
即△BGE是等腰直角三角形;
(2)△BGE的形状是发生改变,此时△BGE是等边三角形;理由如下:
连接GF、DG,如图2所示: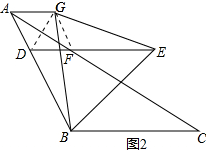
∵AB=BC,∠ABC=120°,
∴∠BAC=∠BCA=30°,
∵AG∥BC,
∴∠BAG=180°-∠ABC=60°,∠ADF=∠ABC=120°,∠AFD=∠BCA=30°,
∴∠BAC=∠BCA,
∴AD=FD,
∵AG=AD,
∴AG=FD,
∴△ADG是等边三角形,四边形ADFG是平行四边形,DG=AD,
∴四边形ADFG是菱形,
∴GF=DF=AD=DG,∠EFG=∠ADF=120°,
∴∠DGF=∠FDG=60°,BD=EF,
∴∠BDG=60°+60°=120°,
∴∠BDG=∠EFG,
在△BDG和△EFG中,
$\left\{\begin{array}{l}{BD=EF}&{\;}\\{∠BGD=∠EFG}&{\;}\\{DG=FG}&{\;}\end{array}\right.$,
∴△BDG≌△EFG(SAS),
∴BG=EG,∠BGD=∠EGF,
∴∠BGE=∠DGF=60°,
∴△BGE是等边三角形.
点评 本题是相似形综合题目,考查了等腰直角三角形的判定与性质、全等三角形的判定与性质、菱形的判定与性质、等边三角形的判定等知识;本题综合性强,难度较大,需要通过作辅助线多次证明三角形全等才能得出结论.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
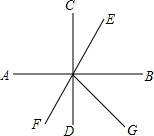 如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )
如图,直线AB、CD、EF相交于点O,且AB⊥CD,OB平分∠EOG,若∠FOD=60°.则∠BOG的度数为( )| A. | 90° | B. | 60° | C. | 30° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
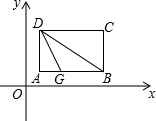 如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=400}\\{60%x-40%y=20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=400}\\{40%x-60%y=20}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=400}\\{60%y-40%x=20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=400}\\{40%-60%x=20}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com