
 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+2��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B����Գ�����x=-1����C��y����һ�㣬��������Ϊm������AC�����߶�AC�Ƶ�A˳ʱ����ת90��õ��߶�AD����AC��ADΪ����������ACED��
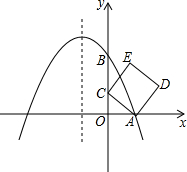
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+2��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B����Գ�����x=-1����C��y����һ�㣬��������Ϊm������AC�����߶�AC�Ƶ�A˳ʱ����ת90��õ��߶�AD����AC��ADΪ����������ACED������ ��1�����ݶ��κ����ĶԳ��Կ������������x�����һ����������꣬�������ߵĽ���ʽΪy=a��x-1����x+3��������0��2���������a��ֵ���ɣ�
��2������E��EF��y�ᣬ����ΪE������֤�����ECE�ա�OAC������ȫ�������ε����ʵõ�BC=OA=1��EF=OC=m���ʴ˿ɵõ���E�����꣬���E��������������ߵĽ���ʽ��⼴�ɣ�
��3�������ֱ��BF�Ľ���ʽ����CE��BFʱ��AC��BF����AC�Ľ���ʽΪy=-$\frac{3}{2}$x+m������A�������������m��ֵ����AC��BFʱ����ֱ��AC�Ľ���ʽΪy=$\frac{2}{3}$x+m������A�������������m��ֵ��
��� �⣺��1����x=0���������ߵĽ���ʽ�ã�y=2��
��B��0��2����
��A��1��0���������ߵĶԳ�����x=-1��
�������߾����㣨-3��0����
�������ߵĽ���ʽΪy=a��x-1����x+3��������0��2������ã�-3a=2����ã�a=-$\frac{2}{3}$��
�������ߵĽ���ʽΪy=-$\frac{2}{3}$x2-$\frac{4}{3}$x+2��
��2������E��EF��y�ᣬ����ΪE��
��ACED������
���ACE=90�㣬CE=AC��
���FCE+��ACO=90�㣮
�֡ߡ�OAC+��ACO=90�㣬
���FCE=��OAC��
�ڡ�FCE�͡�OAC�У�$\left\{\begin{array}{l}{��FCE=��OAC}\\{��EFC=��COA}\\{EC=AC}\end{array}\right.$��
���ECE�ա�OAC��
��BC=OA=1��EF=OC=m��
���E��������m��1+m����
����E��������������ߵĽ���ʽ�ã�-$\frac{2}{3}$m2-$\frac{4}{3}$m+2=m+1�������ã�2m2+7m-3=0����ã�m=$\frac{-7��\sqrt{73}}{4}$��
��3����ͼ2��ʾ����CE��BFʱ��
��BF�Ľ���ʽΪy=kx+2������F���������ã�-3k+2=0�����k=$\frac{2}{3}$��
��BF�Ľ���ʽΪy=$\frac{2}{3}$x+2��
��CE��BF��AC��CE��
��AC��BF��
��AC�Ľ���ʽΪy=-$\frac{3}{2}$x+m��
����A���������ã�-$\frac{3}{2}$+m=0����ã�m=$\frac{3}{2}$��
��ͼ3��ʾ��AC��BFʱ��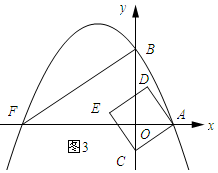
��ֱ��AC�Ľ���ʽΪy=$\frac{2}{3}$x+m������A���������ã�$\frac{2}{3}$+m=0����ã�m=-$\frac{2}{3}$��
����������m��ֵΪ$\frac{3}{2}$��-$\frac{2}{3}$��
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ����Ľ���ʽ�������ε����ʡ�ȫ�������ε����ʺ��ж��������ƽ�е�ֱ�ߵ��ص㡢���ֱ��ֱ�ߵ��ص��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������С�����α߳�Ϊ1�������������У������������Ʊ�Ϊ1��$\sqrt{2}$�����������Ρ�ABC�ס�DEF��
��ͼ������С�����α߳�Ϊ1�������������У������������Ʊ�Ϊ1��$\sqrt{2}$�����������Ρ�ABC�ס�DEF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1cm��2cm��3cm | B�� | 3cm��4cm��5cm | C�� | 4cm��9cm��3cm | D�� | 2cm��1cm��4cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3��$-\frac{1}{3}$ | B�� | -3��$-\sqrt{9}$ | C�� | -3��$\root{3}{-27}$ | D�� | |-3|��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com