
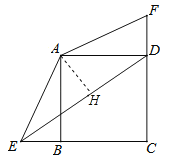
【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据辅助线的性质得到AD=AB,∠ADC=∠ABC=90°,由邻补角的定义得到∠ADF=∠ABE=90°,于是得到结论;
(2)过点A作AH⊥DE于点H,根据勾股定理得到AE=![]() ,ED=
,ED=![]() =5,根据三角形的面积S△AED=
=5,根据三角形的面积S△AED=![]() AD×BA=
AD×BA=![]() ,S△ADE=
,S△ADE=![]() ED×AH=
ED×AH=![]() ,求得AH=1.8,由三角函数的定义即可得到结论.
,求得AH=1.8,由三角函数的定义即可得到结论.
试题解析:(1)正方形ABCD中,∵AD=AB,∠ADC=∠ABC=90°,∴∠ADF=∠ABE=90°,在△ADF与△ABE中,∵AD=AB,∠ADF=∠ABE,DF=BE,∴△ADF≌△ABE;
(2)过点A作AH⊥DE于点H,在Rt△ABE中,∵AB=BC=3,∵BE=1,∴AE=![]() ,ED=
,ED=![]() =5,∵S△AED=
=5,∵S△AED=![]() AD×BA=
AD×BA=![]() ,S△ADE=
,S△ADE=![]() ED×AH=
ED×AH=![]() ,解出AH=1.8,在Rt△AHE中,EH=2.6,∴tan∠AED=
,解出AH=1.8,在Rt△AHE中,EH=2.6,∴tan∠AED=![]() =
=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
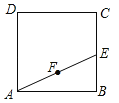
【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形的两边长分别为6 cm、3 cm,则该等腰三角形的周长是( )
A.9 cm B.12 cm C.12 cm或 15 cm D.15 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为 . 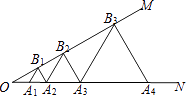
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).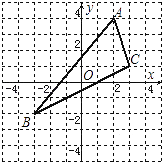
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标.
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com