
【题目】把自然数按如图的次序排列在直角坐标系中,每个点坐标就对应着一个自然数,例如点(0,0)对应的自然数是1,点(1,2)对应的自然数是14,那么点(1,4)对应的自然数是____;点(n,n)对应的自然数是____.

【答案】60, 4n2﹣2n+1.
【解析】
观察图的结构,发现这些数是围成多层正方形,所有奇数的平方数都在第四象限的角平分线上.依此先确定(n,n)坐标的数,再根据图的结构求得坐标(n,n).
解:观察图的结构,发现这些数是围成多层正方形,从内到外每条边数依次+2,所有正方形内自然数个数即(每边自然数个数的平方数)都在第四象限的角平分线上(正方形右下角). 其规律为(n,﹣n)表示的数为(2n+1)2,而且每条边上有2n+1个数,
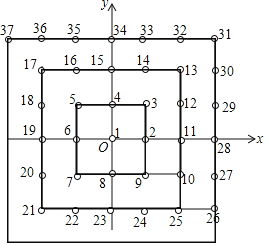
点(1,4)在第四层正方形边上,该层每边有2×4+1=9个数,右下角(4,﹣4)表示的数是81,
所以点(1,4)表示的是第四层从左下角开始顺时针(从81倒数)第21个数,即为81﹣8﹣8﹣5=60,
点(n,﹣n)在第n层正方形边上,该层每边有2n+1个数,右下角(n,﹣n)表示的数是(2n+1)2,
点(n,n)是正方形右上角的数,是从左下角开始顺时针(从(2n+1)2倒数)第6n个数,即为(2n+1)2﹣6n=4n2﹣2n+1.
故答案为:60,4n2﹣2n+1.


科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
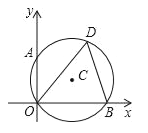
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C上在第一象限内的一点且∠ODB=60°.
(1)求线段AB的长及⊙C的半径;
(2)求B点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)小明解不等式![]() ≤1的过程如下,请指出他解答过程中开始出现错误步骤的序号,并写出正确的解答过程.
≤1的过程如下,请指出他解答过程中开始出现错误步骤的序号,并写出正确的解答过程.
解:去分母得:3(1+x)﹣2(2x+1)≤1……①
去括号得:3+3x﹣4x+1≤1……②
移项得:3x﹣4x≤1﹣3﹣1……③
合并同类项得:﹣x≤﹣3……④
两边都除以﹣1得:x≤3……⑤
解:开始出现错误的步骤序号为 ,正确的解答过程 .
(3)已知实数x,y满足方程组![]() ,求
,求![]() 的平方根;
的平方根;
(4)求不等式组 的整数解.
的整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
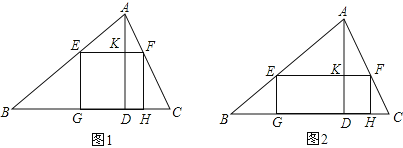
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
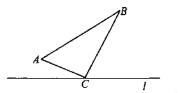
【题目】如图,![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 路径向终点
路径向终点![]() 运动;点
运动;点![]() 从
从![]() 点出发沿
点出发沿![]() 路径向终点
路径向终点![]() 运动.点
运动.点![]() 和
和![]() 分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过
分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过![]() 和
和![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .则点
.则点![]() 运动时间等于____________时,
运动时间等于____________时,![]() 与
与![]() 全等。
全等。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com