
【题目】如图,C为射线AB上一点,AB=30,AC比BC的![]() 多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②AB=4NQ;③当PB=
多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②AB=4NQ;③当PB=![]() BQ时,t=12,其中正确结论的个数是( )
BQ时,t=12,其中正确结论的个数是( )
![]()
A.0B.1C.2D.3
【答案】C
【解析】
根据AC比BC的![]() 多5可分别求出AC与BC的长度,然后分别求出当P与Q重合时,此时t=30s,当P到达B时,此时t=15s,最后分情况讨论点P与Q的位置.
多5可分别求出AC与BC的长度,然后分别求出当P与Q重合时,此时t=30s,当P到达B时,此时t=15s,最后分情况讨论点P与Q的位置.
解:设BC=x,
∴AC=![]() x+5
x+5
∵AC+BC=AB
∴x+![]() x+5=30,
x+5=30,
解得:x=20,
∴BC=20,AC=10,
∴BC=2AC,故①成立,
∵AP=2t,BQ=t,
当0≤t≤15时,
此时点P在线段AB上,
∴BP=AB﹣AP=30﹣2t,
∵M是BP的中点
∴MB=![]() BP=15﹣t
BP=15﹣t
∵QM=MB+BQ,
∴QM=15,
∵N为QM的中点,
∴NQ=![]() QM=
QM=![]() ,
,
∴AB=4NQ,
当15<t≤30时,
此时点P在线段AB外,且点P在Q的左侧,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中点
∴BM=![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N为QM的中点,
∴NQ=![]() QM=
QM=![]() ,
,
∴AB=4NQ,
当t>30时,
此时点P在Q的右侧,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中点
∴BM=![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N为QM的中点,
∴NQ=![]() QM=
QM=![]() ,
,
∴AB=4NQ,
综上所述,AB=4NQ,故②正确,
当0<t≤15,PB=![]() BQ时,此时点P在线段AB上,
BQ时,此时点P在线段AB上,
∴AP=2t,BQ=t
∴PB=AB﹣AP=30﹣2t,
∴30﹣2t=![]() t,
t,
∴t=12,
当15<t≤30,PB=![]() BQ时,此时点P在线段AB外,且点P在Q的左侧,
BQ时,此时点P在线段AB外,且点P在Q的左侧,
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30=![]() t,
t,
t=20,
当t>30时,此时点P在Q的右侧,
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30=![]() t,
t,
t=20,不符合t>30,
综上所述,当PB=![]() BQ时,t=12或20,故③错误;
BQ时,t=12或20,故③错误;
故选:C.
![]()
![]()


科目:初中数学 来源: 题型:
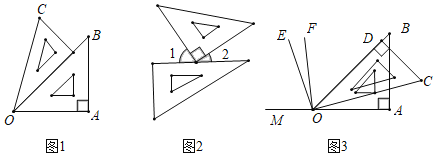
【题目】借助一副三角板,可以得到一些平面图形
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图1所示的曲尺形框框(有三个方向),可以套住图2日历中的三个数,设被框住的三个数中(第一个框框住的最大的数为![]() 、第二个框框住的最大的数为
、第二个框框住的最大的数为![]() 、第三个框框住的最大的数为
、第三个框框住的最大的数为![]() )
)

(1)第一个框框住的三个数的和是: ,第二个框框住的三个数的和是: ,第三个框框住的三个数中的和是: ;
(2)这三个框框住的数的和分别能是81吗?若能,则分别求出最大的数![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
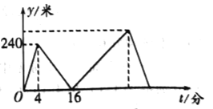
【题目】小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行![]() 米,先到终点的人原地休息.已知小莹先出发
米,先到终点的人原地休息.已知小莹先出发![]() 分钟,在整个步行过程中,两人的距离
分钟,在整个步行过程中,两人的距离![]() (米)与小莹出发的时间
(米)与小莹出发的时间![]() (分)之间的关系如图所示,下列结论:①小莹的步行速度为
(分)之间的关系如图所示,下列结论:①小莹的步行速度为![]() 米/分;②小亮用
米/分;②小亮用![]() 分钟追上小莹;③小亮走完全程用了
分钟追上小莹;③小亮走完全程用了![]() 分钟;④小亮到达终点时,小莹离终点还有
分钟;④小亮到达终点时,小莹离终点还有![]() 米。其中正确的结论有( )
米。其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学要在一块三角形花圃里种植两种不同的花草,同时拟从A点修建一条小路到边BC.
(1)若要使修建小路所用的材料最少,请在下图中画出小路AD;
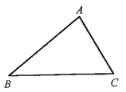
(2)若要使小路两侧种植不同花草的面积相等,请在下图中画出小路AE,其中E点满足的条件是________,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
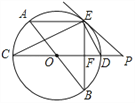
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP.
查看答案和解析>>
科目:初中数学 来源: 题型:
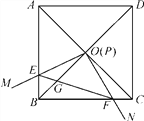
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:(1)EF=![]() OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四边形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OG·BD=AE2+CF2,其中正确的是__.
;(5)OG·BD=AE2+CF2,其中正确的是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB与直线CD相交于O,OB平分∠DOF.

(1)如图,若∠BOF=40°,求∠AOC的度数;
(2)作射线OE,使得∠COE=60°,若∠BOF=x°(![]() ),求∠AOE的度数(用含x的代数式表示).
),求∠AOE的度数(用含x的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com