
【题目】已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2 ![]() ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2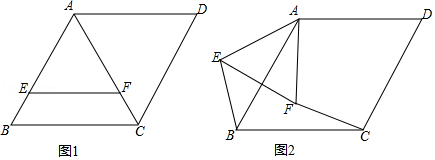
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF= ![]() 时,直接写出旋转角α的度数.
时,直接写出旋转角α的度数.
【答案】
(1)
证明:连接AC,如图2所示:
∵四边形ABCD是菱形,
∴AB=BC=3,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,AB=AC,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
∴∠EAF﹣∠BAF=∠BAC﹣∠BAF,
∴∠BAE=∠CAF,
在△AEB和△AFC中,  ,
,
∴△AEB≌△AFC(SAS),
∴BE=CF

(2)
解:过E点作EM⊥AB于M,如图3所示:
∵∠BAE=45°,则△AEM是等腰直角三角形,
∴EM=AM= ![]() AE=
AE= ![]() ×2
×2 ![]() =2,
=2,
∴BM=AB﹣AM=3﹣2=1,
在Rt△BME中,由勾股定理得:BE= ![]() =
= ![]() =
= ![]() ,
,
由(1)得:CF=BE= ![]()

(3)
解:过E点作EM⊥AB于M,如图4所示,
则∠EMB=∠EMA=90°,
由(1)得:BE=CF= ![]() ,
,
设AM=x,则BM=3﹣x,
由勾股定理得:BM2=BE2﹣BM2,BM2=AE2﹣AM2,
∴BE2﹣BM2=AE2﹣AM2,即( ![]() )2﹣(3﹣x)2=(2
)2﹣(3﹣x)2=(2 ![]() )2﹣x2,
)2﹣x2,
解得:x=0,即点M与A重合,
∴∠BAE=90°,即α=90°;
同理可得:当CF= ![]() 时,α还等于270°;
时,α还等于270°;
综上所述:当CF= ![]() 时,旋转角α的度数为90°或270°
时,旋转角α的度数为90°或270°

【解析】(1)连接AC,证明△AEB≌△AFC,即可得出结论;(2)过E点作EM⊥AB于M,则△AEM是等腰直角三角形,得出EM=AM= ![]() AE=2,求出BM=AB﹣AM=1,在Rt△BME中,由勾股定理求出BE,即可得出CF的长;(3)过E点作EM⊥AB于M,则∠EMB=∠EMA=90°,由(1)得:BE=CF=
AE=2,求出BM=AB﹣AM=1,在Rt△BME中,由勾股定理求出BE,即可得出CF的长;(3)过E点作EM⊥AB于M,则∠EMB=∠EMA=90°,由(1)得:BE=CF= ![]() ,设AM=x,则BM=3﹣x,由勾股定理得出方程,积解方程求出x=0,得出点M与
,设AM=x,则BM=3﹣x,由勾股定理得出方程,积解方程求出x=0,得出点M与
A重合,求出∠BAE=90°,即α=90°;同理可得:当CF= ![]() 时,α还等于270°即可.
时,α还等于270°即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列图形是将正三角形按一定规律排列,第 1 个图形中所有正三角形的个数有 1 个,第 2 个图形中所有正三角形的个数有 5 个,第 3 个图形中所有正三角形的个数有 17 个,则第 5 个图形中所有正三角形的个数有( )
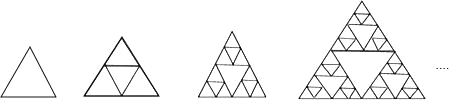
A. 160 B. 161 C. 162 D. 163
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
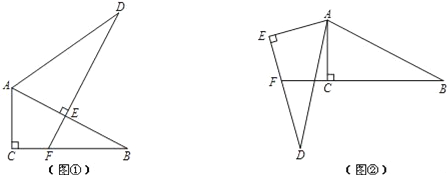
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
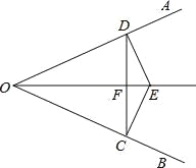
【题目】如图,已知:E 是∠AOB 的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接 CD,且交 OE 于点F.
(1)求证:OD=OC;
(2)求证:OE 是 CD 的垂直平分线;
(3)若∠AOB=60°,请你探究 OE,EF 之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣12a2b2c)(﹣![]() abc2)2=___________;
abc2)2=___________;
(2)(3a2b﹣4ab2﹣5ab﹣1)(﹣2ab2)=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
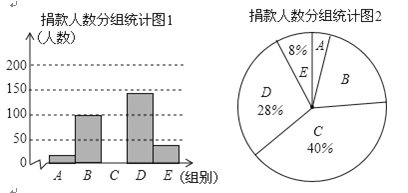
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com