
如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).
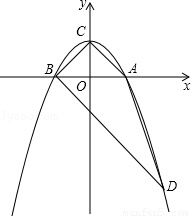
(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由.
解:(1)∵点A(1,0)和点C(0,1)在抛物线y=ax2+b上,
∴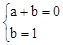 ,解得:
,解得: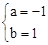 。
。
∴抛物线的解析式为:y=﹣x2+1。
∴抛物线的对称轴为y轴。
∵点B与点A(1,0)关于y轴对称,∴B(﹣1,0)。
(2)设过点A(1,0),C(0,1)的直线解析式为y=kx+b,可得:
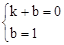 ,解得:
,解得: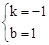 。
。
∴过点A,C的直线解析式为y=﹣x+1。
∵BD∥CA,∴可设直线BD的解析式为y=﹣x+n。
∵点B(﹣1,0)在直线BD上,∴0=1+n,得n=﹣1。
∴直线BD的解析式为:y=﹣x﹣1。
将y=﹣x﹣1代入抛物线的解析式,得:﹣x﹣1=﹣x2+1,解得:x1=2,x2=﹣1。
∵B点横坐标为﹣1,则D点横坐标为2,∴D点纵坐标为y=﹣2﹣1=﹣3。
∴D点坐标为(2,﹣3)。
如图①所示,过点D作DN⊥x轴于点N,
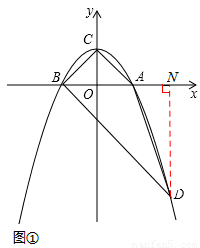
则DN=3,AN=1,BN=3,
在Rt△BDN中,BN=DN=3,
由勾股定理得:BD=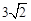 。
。
在Rt△ADN中,DN=3,AN=1,
由勾股定理得:AD=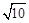 。
。
又OA=OB=OC=1,OC⊥AB,
由勾股定理得:AC=BC=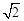 。
。
∴四边形ABCD的周长为:AC+BC+BD+AD=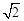 +
+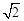 +
+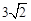 +
+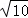 =
=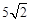 +
+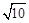 。
。
(3)存在。
假设存在这样的点P,则△BPE与△CBD相似有两种情形:
(I)若△BPE∽△BDC,如图②所示,
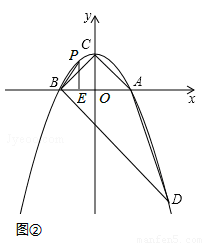
则有 ,即
,即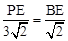 ,∴PE=3BE。
,∴PE=3BE。
设OE=m(m>0),
则E(﹣m,0),BE=1﹣m,PE=3BE=3﹣3m,
∴点P的坐标为(﹣m,3﹣3m)。
∵点P在抛物线y=﹣x2+1上,
∴3﹣3m=﹣(﹣m)2+1,解得m=1或m=2。
当m=1时,点E与点B重合,故舍去;当m=2时,点E在OB左侧,点P在x轴下方,不符合题意,故舍去。
因此,此种情况不存在。
(II)若△EBP∽△BDC,如图③所示,
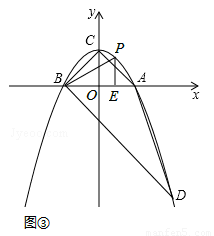
则有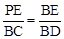 ,即
,即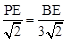 ,∴BE=3PE。
,∴BE=3PE。
设OE=m(m>0),
则E(m,0),BE=1+m,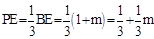 ,
,
∴点P的坐标为(m,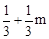 )。
)。
∵点P在抛物线y=﹣x2+1上,
∴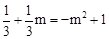 ,解得m=﹣1或m=
,解得m=﹣1或m=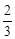 。
。
∵m>0,故m=﹣1舍去,∴m=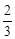 。
。
点P的纵坐标为: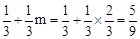 。
。
∴点P的坐标为(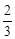 ,
,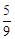 )。
)。
综上所述,存在点P,使以B、P、E为顶点的三角形与△CBD相似,点P的坐标为(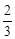 ,
,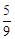 )。
)。
【解析】
试题分析:(1)利用待定系数法求出抛物线的解析式,点B坐标可由对称性质得到,或令y=0,由解析式得到。
(2)求出点D的坐标,然后利用勾股定理分别求出四边形ABCD四个边的长度。
(3)本问为存在型问题。先假设存在,然后按照题意条件求点P的坐标,如果能求出则点P存在,否则不存在.注意三角形相似有两种情形,需要分类讨论。


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 9 |
| 8 |
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com