【题目】已知，如图，E、F分别为矩形ABCD的边AD和BC上的点，AE=CF．求证：BE=DF．
【答案】证明见解析
【解析】证法一：∵四边形ＡＢＣＤ为矩形，
∴ＡＢ＝ＣＤ，∠Ａ＝∠Ｃ＝９０°．…………………………………………４分
在△ＡＢＥ和△ＣＤＦ中，……………………………………………………５分
∵
， ∴△ＡＢＥ≌△ＣＤＦ（ＳＡＳ），……………………８分
∴ＢＥ＝ＤＦ（全等三角形对应边相等）．…………………………………９分
证法二：∵四边形ＡＢＣＤ为矩形，
∴ＡＤ∥ＢＣ，ＡＤ＝ＢＣ，…………………………………………………３分
又∵ＡＥ＝ＣＦ，∴ＡＤ－ＡＥ＝ＢＣ－ＣＦ，……………………………５分
即ＥＤ＝ＢＦ，…………………………………………………………………６分
而ＥＤ∥ＢＦ，
∴四边形ＢＦＤＥ为平行四边形………………………………………………８分
∴ＢＥ＝ＤＦ（平行四边形对边相等）．……………………………………９分
利用全等三角形对应边相等求证
科目：初中数学 来源： 题型：
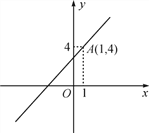
【题目】如图，已知，一次函数y＝kx＋3的图象经过点A（1，4）．
（1）求这个一次函数的解析式；
（2）试判断点B（－1，5），C（0，3），D（2，1）是否在这个一次函数的图象上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的袋子中装有三张分别标有1、2、3数字的卡片（卡片除数字外完全相同）．
（1）从袋中任意抽取一张卡片，则抽出的是偶数的概率为 ；
（2）从袋中任意抽取二张卡片，求被抽取的两张卡片构成两位数是奇数的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列不等式变形正确的是（ ）
A.由a＞b，得ac＞bc
B.由a＞b，得﹣2a＜﹣2b
C.由a＞b，得﹣a＞﹣b
D.由a＞b，得a﹣2＜b﹣2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰△OAB的顶角∠AOB=30°，点B在x轴上，腰OA=4
（1）B点得坐标为： ；
（2）画出△OAB关于y轴对称的图形△OA1B1（不写画法，保留画图痕迹），求出A1与B1的坐标；
（3）求出经过A1点的反比例函数解析式．（注：若涉及无理数，请用根号表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
（1）若两点P（﹣3，m）和Q（1，m）在该函数图象上．求b、m的值；
（2）设该函数的顶点为点B,求出点B 的坐标并求三角形BPQ的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
