
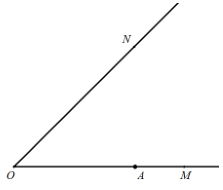
【题目】如图,已知![]() ,
,![]() 为射线
为射线![]() 上一定点,点
上一定点,点![]() 关于射线
关于射线![]() 的对称点为点
的对称点为点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,满足
,满足![]() 为钝角,以点
为钝角,以点![]() 为中心,将线段
为中心,将线段![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,满足点
,满足点![]() 在射线
在射线![]() 的反向延长线上.
的反向延长线上.
(1)依题意补全图形;
(2)当点![]() 在运动过程中,旋转角
在运动过程中,旋转角![]() 是否发生变化?若不变化,请求出
是否发生变化?若不变化,请求出![]() 的值,若变化,请说明理由;
的值,若变化,请说明理由;
(3)从点![]() 向射线
向射线![]() 作垂线,与射线
作垂线,与射线![]() 的反向延长线交于点
的反向延长线交于点![]() ,探究线段
,探究线段![]() 和
和![]() 的数量关系并证明.
的数量关系并证明.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调,乙安装队为B公司安装80台空调,乙安装队提前一天开工,最后与甲安装队恰好同时完成安装任务.已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装多少台空调.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,A(1,0)、C(0,7).
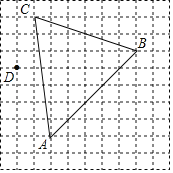
(1)在方格纸中画出平面直角坐标系,写出B点的坐标:B ;
(2)直接写出△ABC的形状: ,直接写出△ABC的面积 ;
(3)若D(﹣1,4),连接BD交AC于E,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助遭受自然灾害的地区,某学校号召同学们自愿捐款,已知第一次捐款总额为5800元,第二次捐款总额6000元,第二次捐款人数比第一次多20人,而且两次人均捐款额正好相等.
|
| |
每桶容积(升) | 20 | 15 |
每桶价格(元) | 5.6 | 4.5 |
(1)求两次各有多少人捐款?
(2)民政部门要求将捐款换成实物,统一运送到灾区.学校决定将捐款用于购买桶装水现有![]() 两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购
两种型号桶装水,上表是这两种桶装水的容积和单价.学校按民政局的救灾规划需订购总容积为40000升的桶装水,用同学们的捐款至少需订购![]() 型水多少桶.
型水多少桶.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 图象
图象![]() 轴上方的部分沿
轴上方的部分沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分保持不变,翻折后的图象与原图象
轴下方,图象的其余部分保持不变,翻折后的图象与原图象![]() 轴下方的部分组成一个“
轴下方的部分组成一个“![]() ”形状的新图象,若直线
”形状的新图象,若直线![]() 与该新图象有两个公共点,则
与该新图象有两个公共点,则![]() 的取值范围为_____.
的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com