
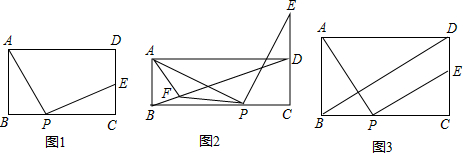
分析 (1)用同角的余角相等得出∠BAP=∠CPE,进而判断出△ABP≌△PCE,即可的得出AB=PC=CD,BP=CE,最后用相等的线段代换即可;
(2)先判断出四边形ABDE是平行四边形则有BD∥AE,即可得到,∠PMN=∠PNM=45°,再判断出,△APF≌△EPD,则有∠AFP=∠DEP,最后用三角形的外角和等角代换即可;
(3)先借助(1)的结论得出PC=AB=2,AD=4-DE,再判断出△CPE∽△CBD,则有$\frac{CP}{CB}=\frac{CE}{CD}$,最后代值解关于DE的方程即可.
解答 解:(1)∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,
∴∠BAP+∠APB=90°,
∵∠APE=90°,
∴∠APB+∠CPE=90°,
∴∠BAP=∠CPE,
在△ABP和△PCE中,$\left\{\begin{array}{l}{∠ABC=∠BCD=90°}\\{∠BAP=∠CPE}\\{AP=EP}\end{array}\right.$,
∴△ABP≌△PCE,
∴AB=PC=CD,BP=CE,
∴AD+DE=BC+DE=BP+PC+DE=CE+CP+DE=CP+CD=2AB;
(2)如图,
∵AB=AF,
∴∠ABF=∠AFB,
∵AB∥DC,
∴∠ABF=∠BDC,
∴∠AFB=∠BDC,
∴∠AFD=∠EDF,
∵AB=CD=DE,AB∥CD,
∴四边形ABDE是平行四边形,
∴BD∥AE,
∵PA=PE,∠APE=90°,
∴∠PAE=∠PEA=45°,
∴∠PMN=∠PNM=45°,
∵BD∥AE,
∴∠FAE+∠AFD=180°,∠FDE+∠AED=180°,
∵∠AFD=∠EDF,
∴∠FAE=∠DEA,
∵∠PAE=∠PEA,
∴∠FAP=∠DEP,
在△APF和△EPD中,$\left\{\begin{array}{l}{AF=DE}\\{∠FAP=∠DEP}\\{PA=PE}\end{array}\right.$,
∴△APF≌△EPD,
∴∠AFP=∠DEP,
∵∠AFD=∠EDF,
∴∠PFD=∠PDF,
在Rt△PCD中,PC=PD,
∴∠CDP=45°,
∴∠ADP=45°,
∴∠ADB=45°-∠PDF=45°-∠PFD,
∵∠AMB=∠PFD+∠APF=45°,
∴∠APF=45°-∠PFD,
∴∠APF=∠ADB;
(3)由(1)知,△ABP≌△PCE,
∴PC=AB=2,由(1)知,AD+DE=2AB=4,
∴AD=4-DE,
∵DB∥PE,
∴△CPE∽△CBD,
∴$\frac{CP}{CB}=\frac{CE}{CD}$,
∵CB=AD=4-DE,CD=AB=2,CE=CD-DE=2-DE,
∴$\frac{2}{4-DE}=\frac{2-DE}{2}$,
∴DE=3+$\sqrt{5}$(由于点E在线段CD上,且CD=2,所以舍去)或DE=3-$\sqrt{5}$,
即:DE=3-$\sqrt{5}$,
故答案为:3-$\sqrt{5}$.
点评 此题是四边形的综合题,主要考查了矩形的性质,全等三角形的判定,等腰三角形的性质和判定,三角形的外角的性质,相似三角形的性质和判定,解本题的关键是判断出△ABP≌△PCE,得出∠APF=∠ADB是解本题的难点.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.21×108 | B. | 321×108 | C. | 3.21×109 | D. | 3.21×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
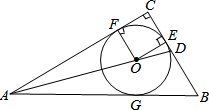 如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径是( )
如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径是( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:单选题
如图,将一副三角板如图放置.若AE∥BC,则∠AFD= ( )
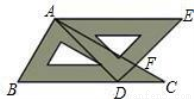
A. 90° B. 85° C. 75° D. 65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com