
【题目】如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC,DE上分别找一点M,N,使△AMN的周长最小,则△AMN的最小周长为 . 
【答案】2 ![]()
【解析】解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.过点A′作EA延长线的垂线,垂足为H,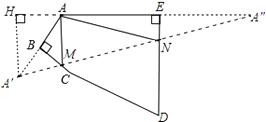
∵AB=BC=1,AE=DE=2,
∴AA′=2BA=2,AA″=2AE=4,
则Rt△A′HA中,∵∠EAB=120°,∴∠HAA′=60°,
∵A′H⊥HA,
∴∠AA′H=30°,
∴AH= ![]() AA′=1,
AA′=1,
∴A′H= ![]() ,
,
A″H=1+4=5,
∴A′A″= ![]() =2
=2 ![]() ,
,
所以答案是:2 ![]() .
.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A. 明年国庆节宁波的天气是晴天B. 小华上学的路上遇到同班同学
C. 任意掷一枚均匀的硬币,正面朝上D. 在学校操场上抛出的篮球会下落
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中的真命题是( )
A. 对角线互相垂直的四边形是菱形B. 中心对称图形都是轴对称图形
C. 两条对角线相等的梯形是等腰梯形D. 等腰梯形是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线. 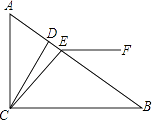
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣22×7﹣(﹣3)×6+5;
(2)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×24÷(﹣2);
)×24÷(﹣2);
(3)56×1 ![]() +56×(﹣
+56×(﹣ ![]() )﹣56×
)﹣56× ![]() ;
;
(4)(﹣1)4﹣ ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①已知∠ACB=∠DCE=90°,AC=BC=4,CE=CD,AE=2,∠CAE=45°,求AD的长.
(2)如图②已知∠ACB=∠DCE=90°,∠ABC=∠DEC=∠CAE=30°,AC=2,AE=4![]() ,求AD的长.
,求AD的长.
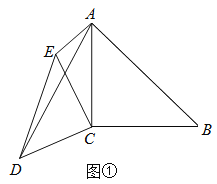

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com