某车队有1辆大车和5辆小车,同时运送一批货物,大车每小时运送货物xt,大车每小时运送的货物是每辆小车每小时运送货物的3倍、设该车队运送货物800t需yh.
(1)写出y与x的函数关系式:______;
(2)当x=12时,y的值是______;
(3)按(2)的工作效率运送800t货物,若要提前10h完成任务,问该车队在不增加大车的情况下,至少要增加几辆小车?
解:(1)根据题意,小车每小时可运送
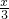
吨货物,
易得这个车队车每小时运送货物为x+

x=
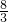
x,
故有y×
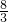
x=800,
化简可得
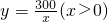
;
(2)由(1)的解析式,
当x=12时,y=
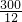
=25;
(3)根据题意,若要提前10h完成任务,即要求y≤15,
代入解析式可得

≤15,
解可得x≥20,
而此时的工作效率为12吨/时,
故至少要增加

=6辆小车.
故答案为:(1)
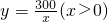
;(2)25.
分析:(1)根据题意,易得这个车队车的工作效率,由效率与时间的关系分析可得答案,
(2)由(1)的结论,将x=12代入可得答案,
(3)根据题意,若要提前10h完成任务,即要求y≤15,代入解析式可得

≤15,解可得x的值,即可得车队的最小工作效率,进而由(2)可得需要增加的工作效率,进而由小车每小时可运送
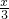
吨货物,计算可得答案.
点评:解答此类问题的关键是根据题意确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

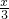 吨货物,
吨货物, x=
x=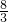 x,
x,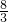 x=800,
x=800,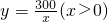 ;
;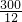 =25;
=25; ≤15,
≤15, =6辆小车.
=6辆小车.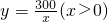 ;(2)25.
;(2)25. ≤15,解可得x的值,即可得车队的最小工作效率,进而由(2)可得需要增加的工作效率,进而由小车每小时可运送
≤15,解可得x的值,即可得车队的最小工作效率,进而由(2)可得需要增加的工作效率,进而由小车每小时可运送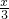 吨货物,计算可得答案.
吨货物,计算可得答案.
